前のチュートリアルでは、オーディオファイルの読み取り、書き込み、再生の簡単な手順を説明しました。余弦関数などの周期関数からオーディオファイルを合成する方法も見ました。このチュートリアルでは、信号への加算、信号の乗算(変調)、およびいくつかの基本的な数学関数を適用して、元の信号への影響を確認する方法を説明します。
2つの信号S1(t)とS2(t)の合計は、任意の時点での値がその瞬間に追加された信号値の合計である信号R(t)になります。ちょうどこのように:
R(t)=S1(t)+ S2(t)
オクターブで2つの信号の合計を再作成し、効果をグラフィカルに確認します。まず、周波数の異なる2つの信号を生成して、合計から生じる信号を確認します。
ステップ1:異なる周波数の2つの信号(oggファイル)を作成する
>>> sig1='cos440.ogg'; %creating the audio file @440 Hz
>> sig2='cos880.ogg'; %creating the audio file @880 Hz
>> fs=44100; %generating the parameters values (Period, sampling frequency and angular frequency)
>> t=0:1/fs:0.02;
>> w1=2*pi*440*t;
>> w2=2*pi*880*t;
>> audiowrite(sig1,cos(w1),fs); %writing the function cos(w) on the files created
>> audiowrite(sig2,cos(w2),fs);
ここでは両方の信号をプロットします。
信号1のプロット(440 Hz)
>> [y1, fs] = audioread(sig1);
>> plot(y1)
信号2(880 Hz)のプロット
>> [y2, fs] = audioread(sig2);
>> plot(y2)
ステップ2:2つの信号を追加する
ここで、前の手順で作成した2つの信号の合計を実行します。
>> sumres=y1+y2;
>> plot(sumres)
結果の信号のプロット
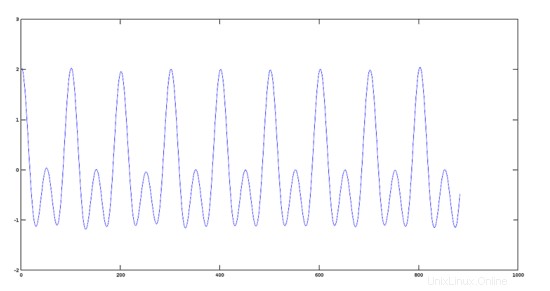
オクターバー効果
オクターバーでは、このエフェクトによって提供されるサウンドは、ミュージシャンが演奏しているノートを、元のノートのサウンドと組み合わせて(プログラムされているように)低いオクターブまたは高いオクターブでエミュレートするため、特徴的です。つまり、2つのノートが表示されます。同じように聞こえます。
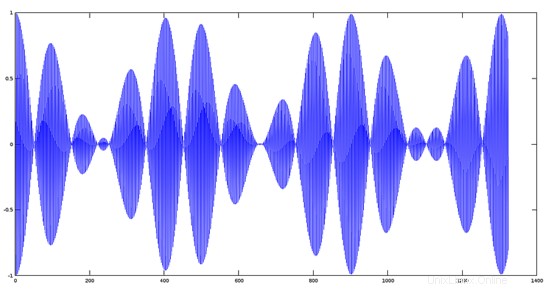
ステップ3:2つの実際の信号を追加する(2つの音楽トラックの例)
この目的のために、グレゴリオ聖歌の2つのトラックを使用します(音声サンプリング)。
アベマリアトラック
まず、Avemariaトラックを読み取ってプロットします:
>> [y1,fs]=audioread('avemaria_.ogg');
>> plot(y1)
賛美歌トラック
さて、賛美歌のトラックを読んでプロットします
>> [y2,fs]=audioread('hymnus.ogg');
>> plot(y2)
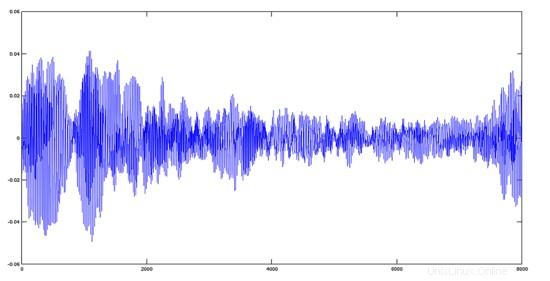
アヴェマリア+賛美歌トラック
>> y='avehymnus.ogg';
>> audiowrite(y, y1+y2, fs);
>> [y, fs]=audioread('avehymnus.ogg');
>> plot(y)
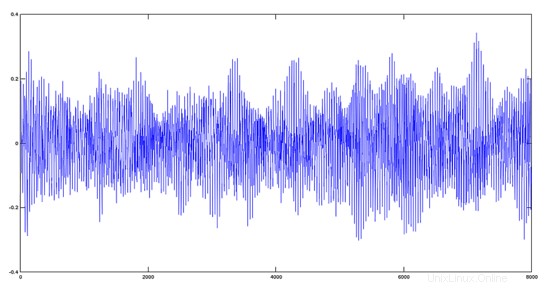
結果は、オーディオの観点から、両方のトラックがミックスされたように聞こえます。
2つの信号の積
2つの信号を乗算するには、合計と同様の方法を使用する必要があります。以前に作成したものと同じファイルを使用しましょう。
>> sig1='cos440.ogg'; %creating the audio file @440 Hz
>> sig2='cos880.ogg'; %creating the audio file @880 Hz
>> product='prod.ogg'; %creating the audio file for product
>> fs=44100; %generating the parameters values (Period, sampling frequency and angular frequency)
>> t=0:1/fs:0.02;
>> w1=2*pi*440*t;
>> w2=2*pi*880*t;
>> audiowrite(sig1, cos(w1), fs); %writing the function cos(w) on the files created
>> audiowrite(sig2, cos(w2), fs);
>> [y1,fs]=audioread(sig1);
>> [y2,fs]=audioread(sig2);
>> audiowrite(product, y1.*y2, fs); %performing the product
>> [yprod,fs]=audioread(product);
>> plot(yprod); %plotting the product
注:この製品は引数ファイルで値から値へと作成されるため、オペランド'。*'を使用する必要があります。詳細については、オクターブの行列を使用した製品操作のマニュアルを参照してください。
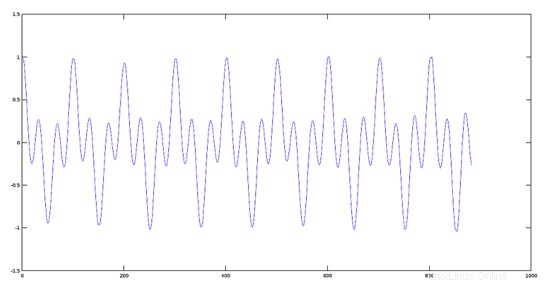
基本周波数の差が大きい2つの信号を乗算した場合のグラフィカルな効果(原理変調の)
ステップ1:
220Hzの周波数の可聴周波数信号を作成します。
>> fs=44100;
>> t=0:1/fs:0.03;
>> w=2*pi*220*t;
>> y1=cos(w);
>> plot(y1);
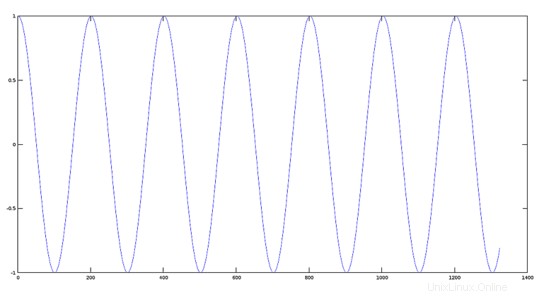
ステップ2:
22000Hzの高周波変調信号を作成します。
>> y2=cos(100*w);
>> plot(y2);
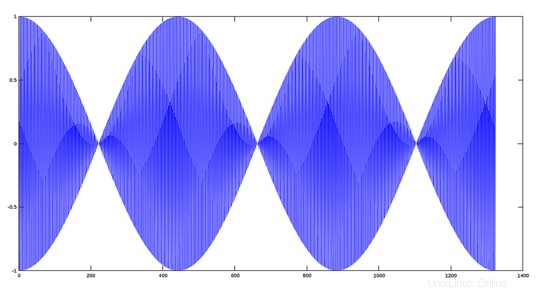
ステップ3:
2つの信号を乗算してプロットします。
>> plot(y1.*y2);
関数にスカラーを乗算する効果は、スコープを変更することと、場合によってはフェーズの符号を変更することと同じです。スカラーKが与えられると、関数F(t)とスカラーの積は次のように定義されます。
R(t)=K * F(t)>> [y,fs]=audioread('cos440.ogg'); %creating the work files
>> res1='coslow.ogg';
>> res2='coshigh.ogg';
>> res3='cosinverted.ogg';
>> K1=0.2; %values of the scalars
>> K2=0.5;
>> K3=-1;
>> audiowrite(res1, K1*y, fs); %product function-scalar
>> audiowrite(res2, K2*y, fs);
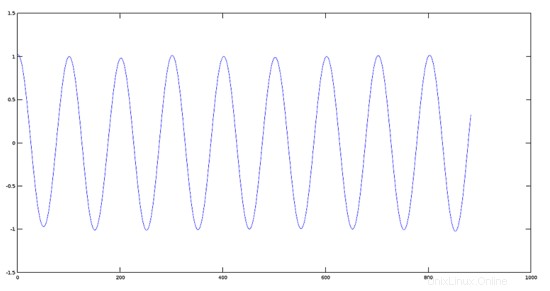
>> audiowrite(res3, K3*y, fs); 元の信号のプロット
>> plot(y)
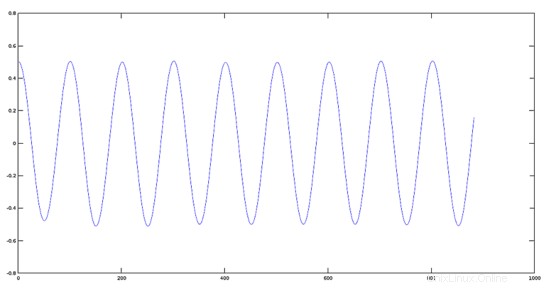
振幅が0.2減少した信号のプロット
>> plot(res1)
振幅が0.5減少した信号のプロット
>> plot(res2)

逆位相の信号のプロット
>> plot(res3)
代数和、積、スカラーによる関数の積などの基本的な数学演算は、スペクトル分析、振幅変調、角度変調など、より高度な演算のバックボーンです。チュートリアルでは、そのような操作を行う方法と、オーディオ信号への影響について説明します。