PythonSciPyチュートリアル-初心者向けガイド

はじめに

コンピューティングは科学研究の重要な部分です。数学、工学、科学、その他の技術的な問題は複雑であり、計算能力と速度が必要です。 Pythonは、技術的な問題を計算で解決するためのSciPyライブラリを提供します。

この記事では、SciPyチュートリアルと、Pythonでコードを実装する方法を例とともに紹介します。

前提条件

• Python2.7またはPython3をインストールしました
• コードを実行するためのPython環境。
• SciPyライブラリがインストールされています。
• NumPyライブラリがインストールされています（ガイド：NumPyのインストール方法に従ってください）。
• プロット用にインストールされたMatplotlibライブラリ（オプション）。

SciPyとは何ですか？

SciPy（ Sci entific Py thon）は、Python用のオープンソースの科学計算モジュールです。 NumPyに基づいて、SciPyには科学的な問題を解決するためのツールが含まれています。科学者は、複雑な問題を解決するための高まるニーズに対応するためにこのライブラリを作成しました。

SciPy vs NumPy

NumPyライブラリ（ Num erical Py thon）は数値計算を行います。 NumPyはデータサイエンス、統計、数学の初歩的な用途をカバーしているため、科学者はこのライブラリを配列の操作に使用します。

SciPyは高度な計算と関数をカバーしています。このライブラリは、より多くのデータサイエンス機能、すべての線形代数関数、および標準の科学アルゴリズムを追加します。

SciPyを使用する理由

SciPyライブラリはNumPyの上に構築され、アレイ上で動作します。 NumPyは評価にCを使用するため、計算能力は高速です。

Pythonの科学スタックは、MATLAB、Octave、Scilab、Fortranに似ています。主な違いは、Pythonは習得と記述が簡単なことです。

SciPyサブパッケージ

SciPyライブラリには、さまざまなサブパッケージのグループがあります。 SciPyモジュールからサブパッケージをインポートする方法は2つあります。

import scipy.<sub package name> as <alias>

または代わりに：

from scipy import <sub package name> as <alias>

どちらのインポート方法でも、エイリアスはオプションです。

SciPy関数

SciPyには、NumPyで利用可能な主要な配列関数の多くと、SciPyサブパッケージから一般的に使用されるモジュールの一部が含まれています。

サブパッケージから関数をインポートするには、次を使用します。

from scipy.<subpackage> import <function>

基本機能

SciPy関数のヘルプと情報を取得するには、 help()を使用します コマンド：

help(<name of function>)

help() コマンドにはパラメータは必要ありません。パラメータなしで実行すると、関数名を入力するプロンプトが表示されます。

Pythonのコマンドに関するヘルプを取得するもう1つの簡単な方法は、コマンド名を記述し、最後に疑問符を付けて、コードを実行することです。

特殊機能

SciPyモジュールの特別な機能には、一般的に使用される計算とアルゴリズムが含まれます。すべての特殊関数は、入力としてNumPy配列を受け入れます。計算は要素ごとです。

specialをインポートするには サブパッケージ、使用：

import scipy.special as special

または代わりに：

from scipy import special

specialから特定の関数をインポートするには サブパッケージ、使用：

from scipy.special import <function name>

階乗

次のコマンドを実行して、任意の数の階乗を評価します。

special.factorial(<integer or array>)

たとえば、10の階乗を見つけるには、次を使用します。

special.factorial(10)

順列と組み合わせ

順列の数を見つけるには、次を使用します：

special.perm(<number of elements>, <number of elements taken>)

たとえば、一度に2つ取得した3つの要素の順列の数を確認するには：

special.perm(6,2)

同様に、次の組み合わせの数を見つけます：

special.comb(<number of elements>, <number of elements taken>, repetition=<True or False>)

繰り返して一度に2つ取られる3つの要素の組み合わせの数を見つけるには、次のように入力します。

special.comb(6,2, repetition=True)

順列と組み合わせは、コンピュータサイエンスの並べ替えアルゴリズムで使用されます。

指数関数

指数関数は、さまざまな基数の指数を評価します。

基数10の指数を次のように計算します：

special.exp10(<integer or array>)

例：

special.exp10([0,1,2])

コンピュータサイエンスでは、2進数の指数関数を使用することがよくあります。

special.exp2(<integer or array>)

2進数の10乗を次のように計算します：

special.exp2(10)

指数の対数和

指数の対数和（LSEまたはLogSumExp）は、機械学習アルゴリズムで使用される近似値です。 LSEを次のように計算します：

special.logsumexp(<integer or array>)

ベッセル関数

ベッセル関数は、波の伝播、信号処理、および静的ポテンシャルの問題に現れます。次のコマンドで第1種のベッセル関数を見つけます：

special.jn(<integer order>, <integer or array>)

フルスタックを利用して、ベッセル関数を視覚化します。第1種の2次ベッセル関数を見つけるには、次を使用します。

#import stack
import scipy.special as special
import matplotlib.pyplot as plt
import numpy as np
#The X-axis
x = np.linspace(1,50,100)
#Bessel function of the first kind order two
jn1 = special.jn(2,x)

結果をプロットします：

#Plotting
plt.title('Bessel function first kind order two')
plt.plot(x, jn1)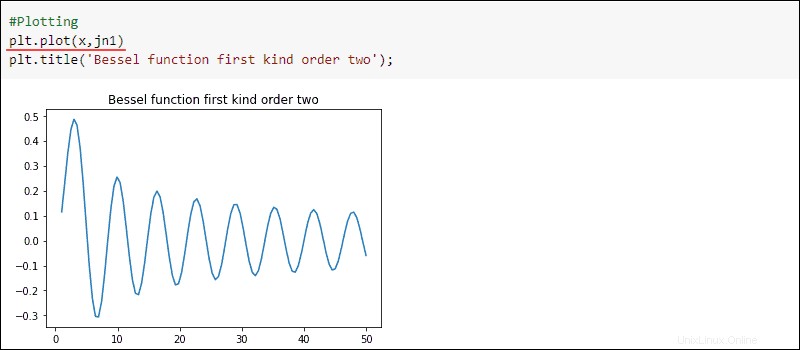

統合およびODE機能

SciPyは、定積分を使用した計算用のサブパッケージを提供します。 integrateをインポートするには サブパッケージ、使用：

import scipy.integrate as integrate

または代わりに：

from scipy import integrate

サブパッケージから特定の関数をインポートするintegrate と：

from scipy.integrate import <function name>

一般的な統合

quadを使用して単一の変数積分を計算します integrateからの関数 サブパッケージ：

integrate.quad(<function>, <lower limit>, <upper limit>)

function 入力はラムダ関数を使用して定義されます。

たとえば、関数x +1の0と1の間の定積分を計算するには：

from scipy import integrate
f = lambda x: x+1
integrate.quad(f, 0, 1)

出力には2つの値が表示されます。最初の値は評価された積分であり、2番目の値は推定の誤差です。

最適化関数

SciPyには、関数の最小値または最大値を見つけるための最適化サブパッケージがあります。 optimize サブパッケージには、ローカルおよびグローバルの最適値を見つけるためのソルバーとアルゴリズムが含まれています。

最適化サブパッケージをインポートするには：

from scipy import optimize

または使用：

import scipy.optimize as optimize

サブパッケージから特定の関数をインポートするにはoptimize 、実行：

from scipy.optimize import <function name>

関数を最小化する

関数の最小値を見つけることは、アルゴリズムの損失（またはエラー）を下げるために機械学習で使用されます。

たとえば、関数を作成して最小値を見つけることができます。これを行うには、 fminを使用します optimizeからの関数 SciPyのサブパッケージ：

#Import stack
import numpy as np
from scipy import optimize
#Defining inverse sine function
def f(x):
    return -np.sin(x)
#X-axis
x = np.linspace(0,5,100)
#Starting point
start = 3
#Simplex algorithm for optimization
optimized = optimize.fmin(f,start)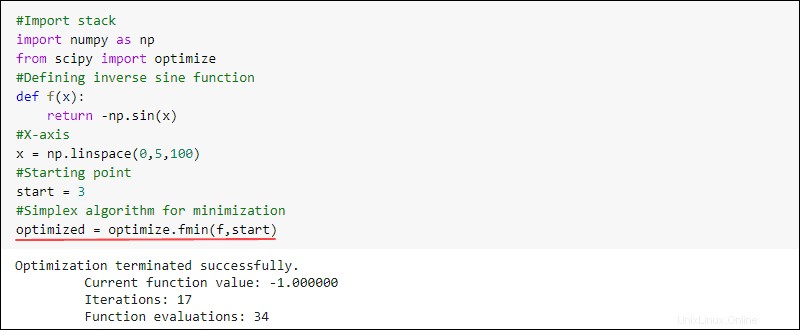

結果をプロットするには、次のコマンドを実行します：

import matplotlib.pyplot as plt
plt.plot(x, f(x))
plt.scatter(start,f(start))
plt.scatter(optimized, f(optimized))
plt.legend(['Function -sin(x)', 'Starting point', 'Optimized minimum'])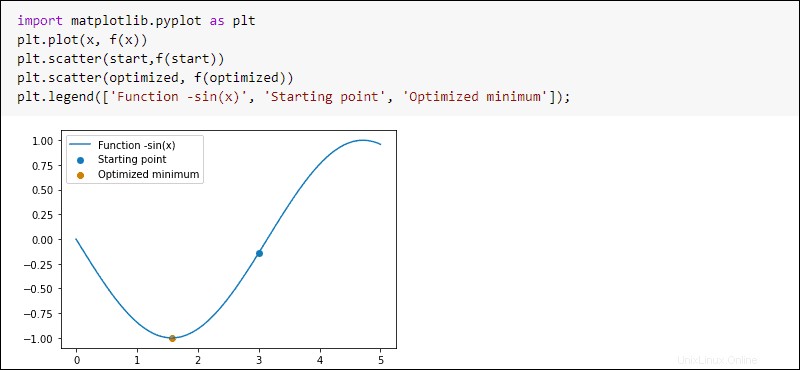

フーリエ変換関数

SciPyには、 fftpackと呼ばれるフーリエ変換関数のサブパッケージが含まれています 。変換は離散フーリエ変換（DFT）です。すべての変換は、高速フーリエ変換（FFT）アルゴリズムを使用して適用されます。

fftpackをインポートするには サブパッケージ、使用：

import scipy.fftpack as fftpack

または：

from scipy import fftpack

高速フーリエ変換

例として、3つの正弦波の合計として周期関数を作成します。

import numpy as np
freq_samp = 100
#Time
t = np.linspace(0, 1, freq_samp*2, endpoint = False )
#Frequencies
f1, f2, f3 = 1, 5, 20
#Amplitudes
A1, A2, A3 = 3, 2, 1
x1 = A1*np.sin(f1*2*np.pi*t)
x2 = A2*np.sin(f2*2*np.pi*t)
x3 = A3*np.sin(f3*2*np.pi*t)
#Sum of waves
x = x1+x2+x3

matplotlibを使用して波をプロットします ：

import matplotlib.pyplot as plt
plt.subplot(2,1,1)
plt.plot(t,x1,t,x2,t,x3)
plt.subplot(2,1,2)
plt.plot(t,x)
plt.xlabel('Time (s)')
plt.ylabel('Amplitude');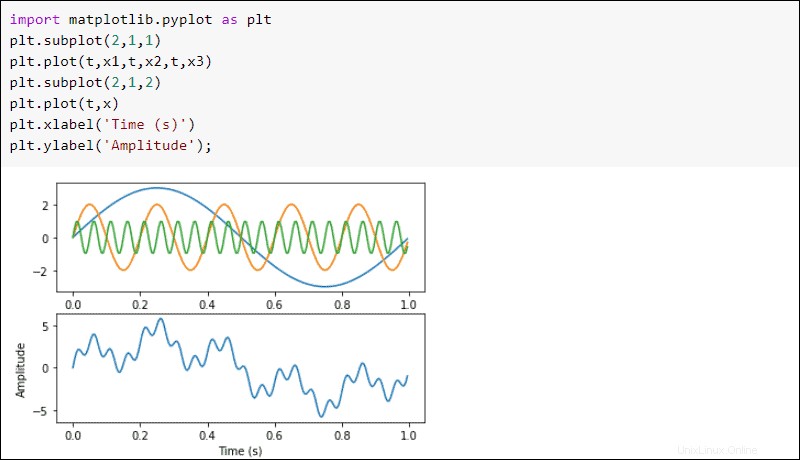

次に、 fftを適用します およびfftfreq fftpackの関数 信号のフーリエ変換を行います。

from scipy import fftpack
A = fftpack.fft(x)
freq = fftpack.fftfreq(len(x))*freq_samp*2

結果をプロットして、周波数領域を確認します。

plt.stem(freq,np.abs(A)/freq_samp,use_line_collection=True)
plt.xlim(-25,25)
plt.xlabel('Frequency (Hz)')
plt.ylabel('Amplitude')
plt.grid()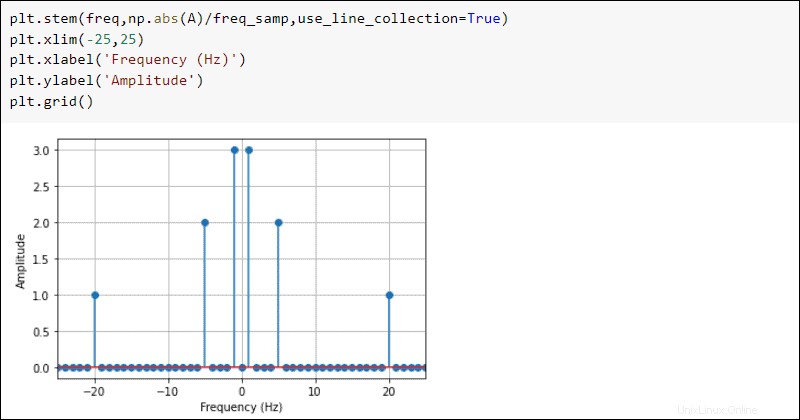

信号処理機能

サブパッケージsignal 信号処理で使用される機能が含まれています。 signalをインポートするには 、実行：

import scipy.signal as signal

または代わりに：

from scipy import signal

畳み込み

信号処理の一般的なタスクは畳み込みです。 SciPyサブパッケージsignal convolveという機能があります このタスクを実行します。たとえば、周波数の異なる2つの信号を作成します。

import numpy as np
#Time
t = np.linspace(0,1,100)
#Frequency
f1, f2 = 5, 2
#Two signals of different frequencies
first_signal = np.sin(f1*2*np.pi*t)
second_signal = np.sin(f2*2*np.pi*t)

信号をプロットします：

import matplotlib.pyplot as plt
#Plotting both signals
plt.subplot(2,1,1)
plt.plot(t, first_signal)
plt.subplot(2,1,2)
plt.plot(t, second_signal)
plt.ylabel('Amplitude')
plt.xlabel('Time (s)')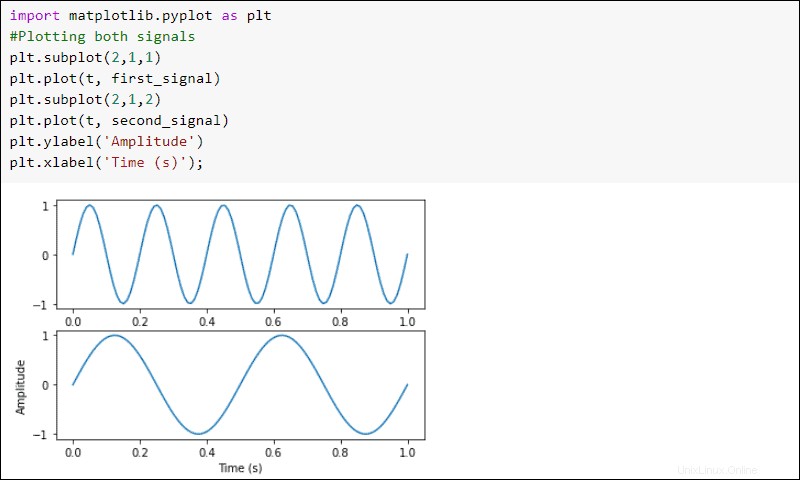

signalをインポートします scipyのサブパッケージ 。 convolveを使用します signalからの機能 2つの信号を畳み込むサブパッケージ：

#Importing the signal subpackage
from scipy import signal
#Convolving two signals
convolution = signal.convolve(first_signal, second_signal, mode='same')

結果をプロットします：

#Plotting the result
plt.plot(t, convolution)
plt.xlabel('Time (s)')
plt.ylabel('Amplitude')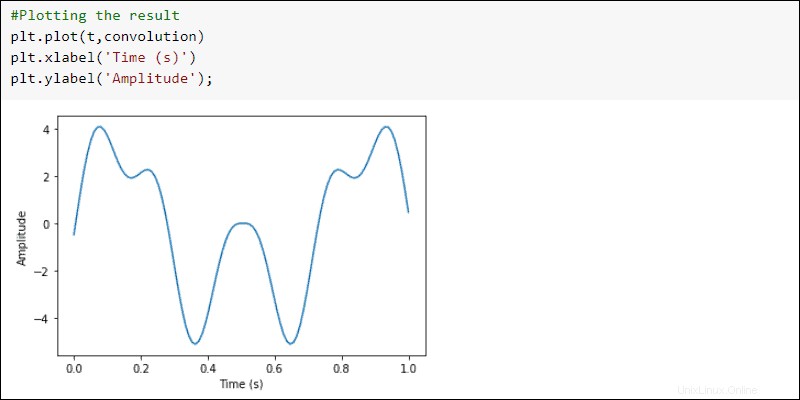

補間関数

補間は、数値解析フィールドで2点間の値を一般化するために使用されます。 SciPyにはinterpolateがあります 補間関数とアルゴリズムを備えたサブパッケージ。

interpolateをインポートします サブパッケージ：

import scipy.interpolate as interpolate

または：

from scipy import interpolate

1次元補間

SciPyinterpolate サブパッケージにはinterp1dがあります データの1次元補間のための関数。例として、おもちゃを作成します numpyを使用したデータ ：

import numpy as np
#Create toy data
x = np.arange(0,10,0.5)
y = np.sin(x)

interp1dを使用してデータを補間します interpolateから サブパッケージ：

from scipy import interpolate
#Interpolate
f = interpolate.interp1d(x, y)
#Create interpolation function
x_i = np.arange(0,10,3)
y_i = f(x_i)

結果をプロットします：

#Plot results
plt.scatter(x,y)
plt.plot(x_i, y_i)
plt.legend(['Interpolation', 'Data points'])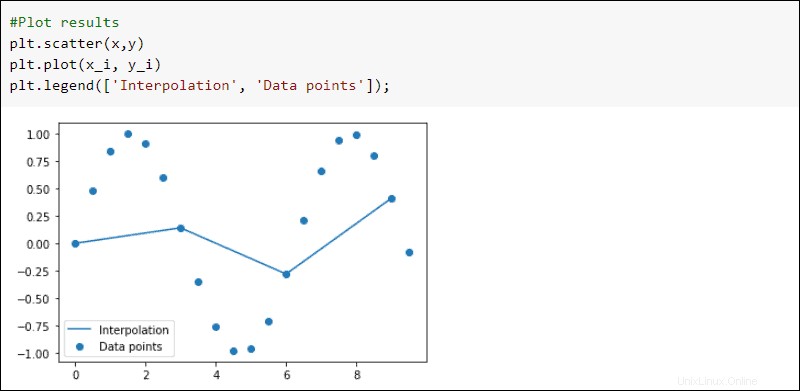

線形代数

SciPyには、フル機能の線形代数サブパッケージがあります。 SciPy線形代数サブパッケージは、ATLAS LAPACKおよびBLASライブラリで最適化されており、計算が高速化されています。

SciPyから線形代数パッケージをインポートするには、次のコマンドを実行します。

import scipy.linalg as linalg

または使用：

from scipy import linalg

すべての線形代数関数は、入力にNumPy配列を必要とします。

行列式

detを使用して行列式を計算します linalgから サブパッケージ：

linalg.det(<numpy array>)

例：

import numpy as np
#Generate a 2D array
A = np.array([[1,2],[3, 4]])
from scipy import linalg
#Calculate the determinant
linalg.det(A)

逆行列

invを使用して、逆行列を決定します ：

linalg.inv(<numpy array>)

例：

import numpy as np
#Generate a 2D array
A = np.array([[1,2],[3,4]])
from scipy import linalg
#Calculate the inverse matrix
linalg.inv(A)

固有ベクトルと固有値

固有ベクトルと固有値は行列分解法です。固有値-固有ベクトル問題は、一般的に実装されている線形代数問題です。

eig 関数は、行列の固有値と固有ベクトルを見つけます。

linalg.eig(<numpy array>)

出力は2つの配列を返します。 1つ目は固有値を含み、2つ目は指定された行列の固有ベクトルを含みます。例：

import numpy as np
#Generate a 2D array
A = np.array([[1,2],[3, 4]])
from scipy import linalg
#Calculate the eigenvalues and eigenvectors
linalg.eig(A)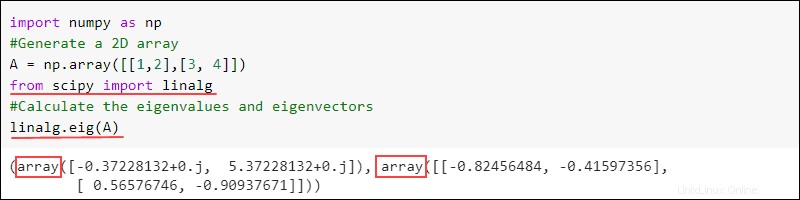

空間データ構造とアルゴリズム

空間データ構造は、ポイント、ライン、およびサーフェスで構成されるオブジェクトです。 SciPyには、多くの科学分野に適用されるため、空間データ構造のアルゴリズムがあります。

spatialをインポートします SciPyのサブパッケージ：

import scipy.spatial as spatial

または：

from scipy import spatial

空間アルゴリズムの注目すべき例はボロノイ図です。与えられた点のセットに対して、ボロノイマップは平面を領域に分割します。新しいポイントがリージョンに分類される場合、そのリージョン内のポイントが最近傍になります。

例として、20個のランダムな点からボロノイ図を作成します。

from scipy.spatial import Voronoi
import numpy as np
points = np.random.rand(20,2)
voronoi = Voronoi(points)
from scipy.spatial import voronoi_plot_2d
fig = voronoi_plot_2d(voronoi,show_vertices=False)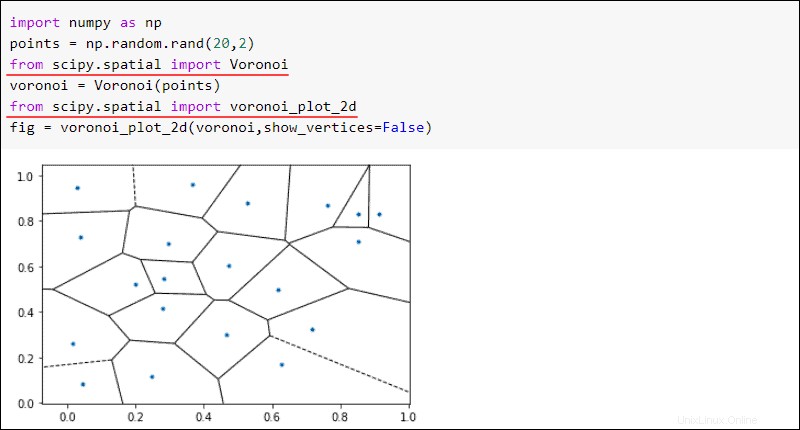

画像処理

SciPyには、さまざまなn次元画像処理用のサブパッケージがあります。 ndimageをインポートするには サブパッケージ、実行：

import scipy.ndimage as ndimage

または使用：

from scipy import ndimage

SciPymisc サブパッケージには、デモンストレーション用のサンプルイメージが含まれています。 miscをインポートするには サブパッケージして画像を表示します：

from scipy import misc
from matplotlib import pyplot as plt
raccoon = misc.face()
#show image
plt.imshow(raccoon)
plt.show()

ndimageをインポートします サブパッケージしてuniform_filterを適用します 画像に。画像を表示して結果を確認します：

from scipy import ndimage
filtered = ndimage.uniform_filter(raccoon)
plt.imshow(filtered)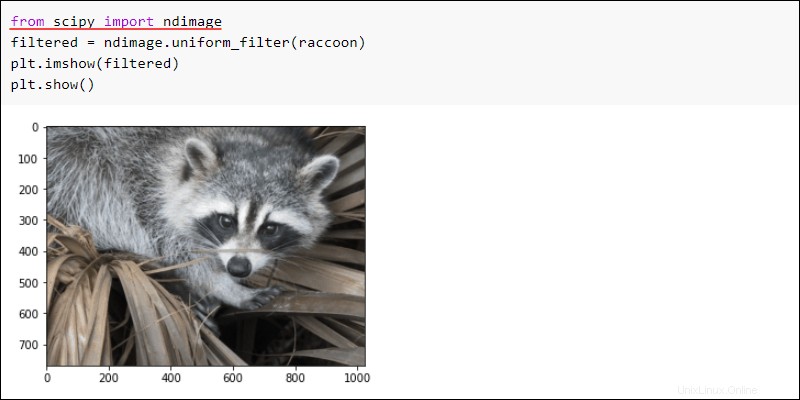

ファイルIO（ファイル入力/出力パッケージ）

SciPyには、 ioというファイル入力および出力サブパッケージがあります。 。 io サブパッケージは、Fortran、MATLAB、IDLなどのさまざまな科学計算プログラムや言語からのデータ形式の読み取りと書き込みに使用されます。

ioをインポートします SciPyのサブパッケージ：

import scipy.io as sio

または使用：

from scipy import io as sio