Linux デスクトップに最適な 20 のコンピューター代数システム

計算問題を解決することは、コンピューターの発明の背後にある最初のインスピレーションでした。現代のコンピューターはその誕生以来長い道のりを歩んできましたが、複雑な計算を解決する上で事実上の役割を果たしています。コンピューター代数システム (CAS) は、複雑な方程式や計算システムを手動で操作することなく、現代の複雑な計算問題に取り組むことができるソフトウェア環境です。これらのコンピューター代数システムは、従来の数学者のように数式を操作し、潜在的なエラーを効果的に阻止します。 Linux には、汎用と特殊の両方のさまざまなコンピューター代数システムがあります。

Linux 用の最高のコンピューター代数システム

CAS の主な機能は、数値計算、記号計算、データ分析、およびデータ視覚化を実行することです。その広範なドメインにより、さまざまな種類のアプリケーションを扱う Linux 用のさまざまなコンピューター代数システムが存在します。私たちの編集者は、数学者、データサイエンスの専門家、または高等研究目的で使用できる 20 の最高のコンピューター代数システムの概要を説明しました。

1. SageMath

SageMath は、広範な機能セットを備えた Linux 用のオープンソースのコンピューター代数システムであり、現代の数学の問題を処理するための優れたソリューションとなっています。 NumPy、SciPy、matplotlib、Sympy、Maxima、GAP、FLINT、R など、既存の人気のあるオープンソースパッケージの上に構築されています。このプロジェクトは、Magma、Maple、Mathematica、および Matlab に代わる実行可能な代替物になることを目指しており、その期待に十分応えています。

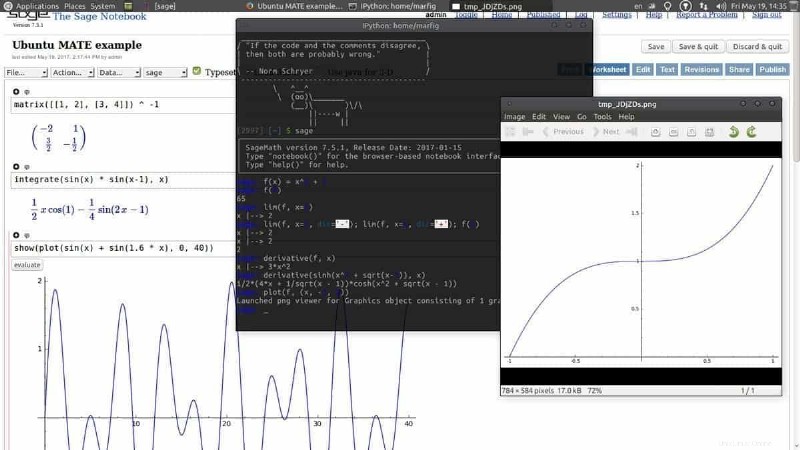
SageMath の機能

SageMath は、Python と Cython を利用して、インターフェースやラッパーを通じて、基盤となるプロジェクトの力を便利に活用します。
Chrome、Opera、Firefox、Safari、Konqueror と互換性のある革新的で使いやすいノートブックドキュメントインターフェースが付属しています。
SageMath は、iPython シェルの上に構築されたテキストベースのコマンドラインインターフェースも提供します。
異なるプロセッサアーキテクチャを使用した並列処理をサポートし、Mathematica、Magma、および Maple へのインターフェイスを提供します。
SageMath を使用すると、ユーザーは Sage を LaTeX ドキュメント内に埋め込み、スライダーを計算入力として使用できます。

2. MATLAB

MATLAB は、現代のコンピューター代数システムの聖杯として多くの人に歓迎されています。数学的研究や実世界のデータ分析に関しては、事実上の CAS として証明されています。 MATLAB が提供する機能は広範であり、詳細を説明するには専用のガイドが必要です。多くの人にとっての MATLAB の最大のセールスポイントは、その一流のドキュメントです。また、ほとんどすべての数学関数が既に実装されており、すぐに使用できます。

MATLAB の機能

MATLAB では、行列の操作、関数のプロット、データの操作、サードパーティのアプリケーションやスクリプトとのインターフェース、グラフィックシミュレーションなどを行うことができます。
この CAS システムは、線形および非線形代数、統計、最適化、連立方程式、フーリエ解析、ラプラス変換のための関数とアルゴリズムのモノリシックな選択を提供します。
コマンドラインインターフェース、GUI インターフェース、カスタムインターフェース作成機能など、幅広いインターフェースオプションをサポートしています。
このソフトウェアはプロプライエタリであり、macOS、Windows、Linux、BSD システムなど、ほぼすべての主要システムで動作します。

3. Scilab

Scilab は、Linux 用の最高のコンピューター代数システムの 1 つで、科学計算をこれまで以上に簡単にする高度な機能を幅広く提供します。 90 年代に開発されて以来、効果的な CAS ソリューションであることが証明されており、現代の科学事業において重要な役割を果たしています。 Scilab は、研究者、ビジネスアナリスト、数学者がわずか数行のコードで現実世界の計算問題を解決できる高レベルのプログラミング環境を提供します。

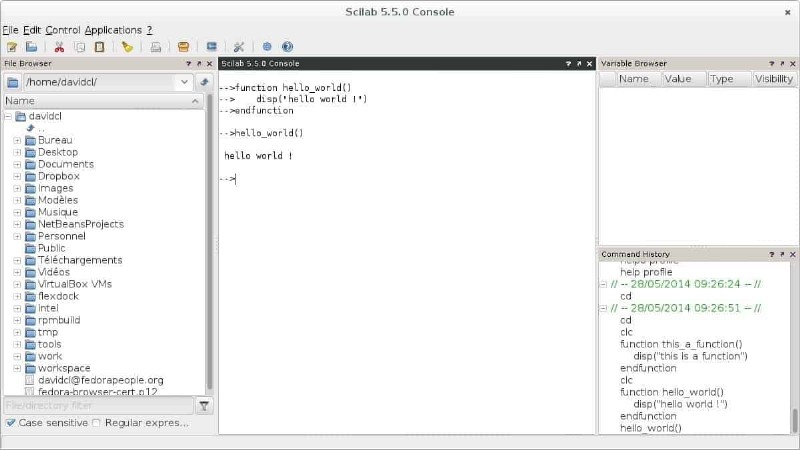
Scilab の機能

Scilab を使用すると、研究者は新しいデータ型と演算の両方を定義して、オーバーロードを使用してそれらを実行し、MATLAB と同様の構文を使用できます。
このオープンソースの Linux 用 CAS システムは、線形代数、多項式、スパース行列、有理関数、2 次元および 3 次元グラフィックス、アニメーションなどをサポートしています。
Scilab には、LaTeX/MathML、SciNotes テキストエディター、LMI 最適化、高度なスクリプト機能のサポートが組み込まれています。
Scilab が提供する統一された一貫性のある API は、ほんの一握りのコンピューター代数システムに匹敵します。

4.オクターブ

GNU Octave は、その豊富で使いやすい機能のおかげで、世界中の学生や専門家に使用されている最も人気のある Linux コンピューター代数システムの 1 つです。これは、デフォルトのプロット機能と視覚化機能を備えた強力なプログラミング言語です。この言語は MATLAB と互換性があり、ユーザーは便利なコマンドラインインターフェイスを使用して線形および非線形の計算問題を解くことができます。また、グラフィカルインターフェイスを好むユーザー向けに、Qt ベースの GUI も提供しています。

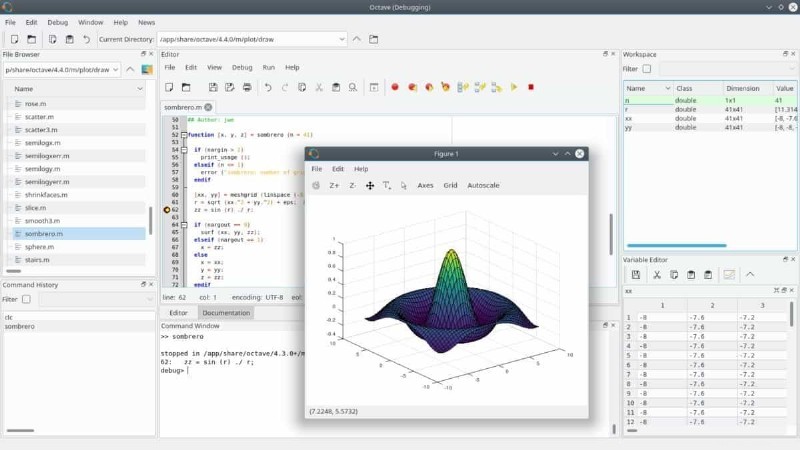
オクターブの特徴

Octave は、線形方程式と非線形方程式の解法、多項式の操作、積分、微分計算、ベクトル、行列など、包括的な数学的手法を提供します。
このオープンソースの CAS は高度なカスタマイズが可能で、ユーザー定義関数や C、C++、Fortran などの言語で記述された動的モジュールを使用して拡張できます。
GUI インターフェースは使いやすく、IDE と並んで Qt ベース上にあります。
Octave は C++ を使用して記述されており、プログラマーは C++ プログラム内で直接 Octave ソースを使用できます。

5.マキシマ

Maxima は、このガイドで取り上げる最も古い Linux コンピューター代数システムの 1 つです。このプロジェクトは 60 年代に MIT のラボで開始され、その広範な人気と悪名高い強力な機能セットにより、今日でも繁栄を続けています。このシステムは、微分、積分、テイラー級数、ラプラス変換、微分方程式、多項式、集合、リスト、ベクトル、行列、テンソルと並んで線形方程式系を含む、記号表現と数値表現に取り組むように設計されています。

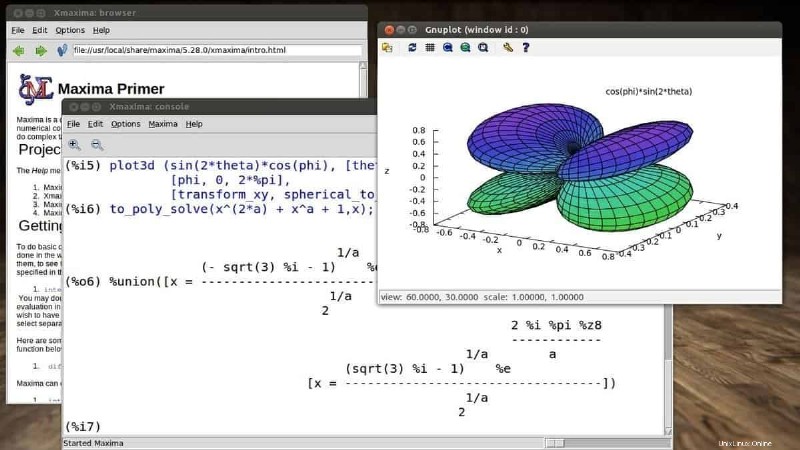
マキシマの特徴

Maxima は、堅牢な正確な分数、任意精度の整数、および浮動小数点数により、Linux 用のほとんどのコンピューター代数システムよりも非常に正確な数値結果を提供します。
Common Lisp プログラミング言語を使用して記述されており、ALGOL に似た構文を備えた完全なプログラミング言語を提供します。
Maxima は、Lisp スタイルのセマンティクスを利用して、コンピュータ代数の教育とプログラミングのレッスンを容易にします。
wxMaxima、TeXmacs、SAGE など、さまざまなグラフィカルユーザーインターフェイス (GUI) をサポートしています。

6. SymPy

SymPy は、記号数学を操作するためのオープンソースの Python ライブラリです。ユーザーは、スタンドアロンアプリケーション、Web 上でのライブ、または他のプログラム内のライブラリとして使用できます。 BSD ライセンスにより、SymPy は間違いなく、オープンソースの愛好家や無料のコンピューター代数システムを探している数学者にとって最高のコンピューター代数システムの 1 つです。 SymPy は定期的にメンテナンスされており、新しい更新が非常に頻繁に展開されるため、プロのアナリストと学者の両方にとって適切な選択肢となっています。

SymPy の機能

多項式、代数、微分、差、連立方程式、ディオファントス方程式を微積分、離散数学、幾何学、行列と一緒に解くことができます。
プロット機能には、座標モード、幾何学的エンティティ、2D および 3D グラフィックス、色、Matplotlib サポートが含まれます。
SymPy には、Hill cipher、RSA、ElGamal 暗号化など、多数の暗号化機能が組み込まれています。
SymPy のオープンソースの性質により、開発者は最新の計算プロジェクトの要件を満たすようにアプリケーションを拡張できます。

7.単数

SINGULAR は、可換代数、代数幾何学、特異点理論などの多項式問題を処理するための最高のコンピューター代数システムの 1 つです。 Groebner resp を計算するための最速のアルゴリズム実装が付属しています。 Mora のアルゴリズムと Buchberger のアルゴリズムを含む標準ベース。 SINGULAR は、多項式因数分解、Syzygy、自由解像度計算、特性集合、結果などの機能も提供します。

SINGULAR の機能

SINGULAR の主な計算対象は、さまざまな分野での基底環またはローカリゼーションの大規模な選択をカバーするイデアルとモジュールです。
C++ で記述されたさまざまな実装済みアルゴリズムが付属しているため、はるかに高速で最適化されたパフォーマンスが提供されます。
この CAS 環境のプログラミング言語は C に似ており、従来のプログラミング言語の予備知識がある人にとっては直感的です。
SINGULAR は、豊富なドキュメント、便利なライブラリの大規模なセット、Emacs インターフェース、オープンソースサポートとともに動的モジュールをロードする機能を提供します。

8.メープル

Maple は、世界中の企業で使用されている主要な Linux コンピューター代数システムの 1 つです。これは、記号計算と数値計算に重点を置いて設計した Maplesoft によって開発および販売されています。また、高度なコンピューティングタスクを支援する高レベルのプログラミング言語も提供します。 Maple には、科学計算を簡単に、そしてより多くの人々がアクセスできるようにするための幅広いツールが搭載されています。

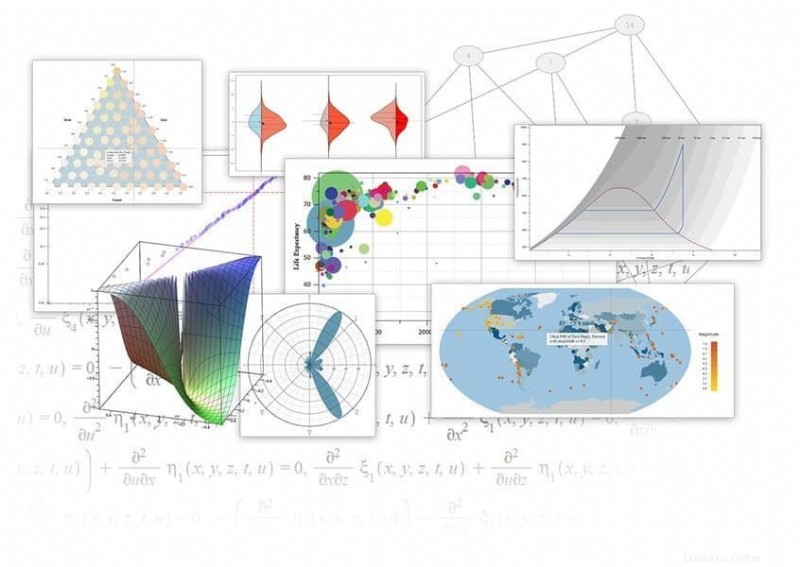
メイプルの特徴

Maple には、初等および特殊な数学関数用の専用ライブラリが付属しており、正確な結果を伴う記号計算および数値計算を提供します。
ディオファントス方程式、ODE、PDE、DAE、DDE、再帰関係など、幅広い方程式を処理できます。
Maple には、データの操作、分析、視覚化のための堅牢なツールと、確率および組み合わせ問題のためのツールが備わっています。
Maple では、正規表現を使用したテキストマイニングが可能で、財務計算、時系列、並列プログラミング、その他多くの革新的な機能がサポートされています。

9.マコーレー2

Macaulay2 は、代数幾何学と可換代数を扱う研究者にとって最も著名なコンピューター代数システムの 1 つです。これは、伝統的および未来的な数学研究の問題に対する新しいソリューションの開発を支援する多数の組み込み機能を備えた、かなり最新の CAS です。数値代数と記号代数に取り組む独自の高水準プログラミング言語を実装し、オープンソース GNU GPL ライセンスの下でリリースされています。

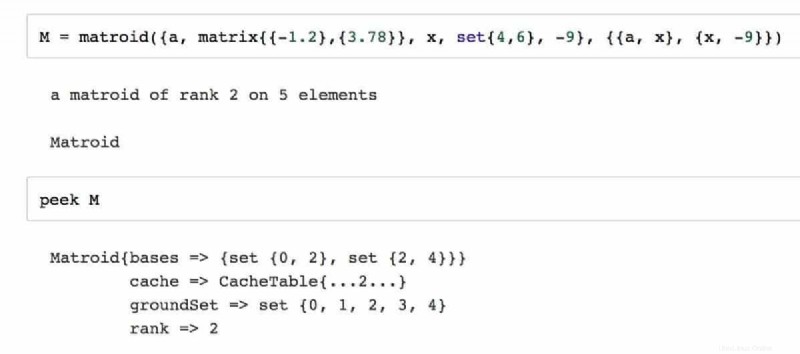
Macaulay2 の特徴

Macaulay2 は、ガロア体、数体、多項式環、ワイル代数、商環、準同型写像、段階的加群、連鎖複体などの高レベルの数学オブジェクトの効率的な計算をサポートしています。
この CAS のインタープリター型プログラミング言語はシンプルですが強力で、各オブジェクトに型を割り当てます。
数学的アルゴリズムは C++ を使用して実装されるため、高速で最適化されたパフォーマンスが得られます。
このクロスプラットフォーム CAS はオープンソースであり、開発者は必要に応じてソフトウェアを拡張できます。

10.カダブラ

場の理論の問題に最適なコンピューター代数システムを探している場合、Cadabra は最適な選択肢の 1 つです。これは、場の理論の研究者を対象とした最新の記号的コンピューター代数システム (CAS) であり、その目的を支援するための広範な機能セットを提供します。 Cadabra は、Bianchi および Schouten 恒等式を利用することにより、テンソル多項式の簡略化を非常に効果的に処理し、フェルミオンおよび反交換変数、クリフォード代数、Fierz 変換、および他の多くの問題にも使用できます。

カダブラの特徴

Cadabra には、便利なコマンドラインインターフェースと、シンプルで直感的なグラフィカルユーザーインターフェースが付属しています。
プログラミング性が高く、Python プログラミング言語を使用して簡単に拡張できる
Cadabra は、Sympy とシームレスに使用できるスタンドアロンの GUI ノートブックインターフェースを備えています。
このクロスプラットフォームのコンピューター代数システムは完全にオープンソースであり、ソースは変更可能です。

11. Wolfram Mathematica

Wolfram Mathematica は、ジオメトリ、データサイエンス、ビジュアライゼーション、ニューラルネットワーク、画像処理など、技術計算のほとんどの分野を網羅する現代のコンピュータ代数システムです。研究者と専門家の両方によって、幅広いタスクに非常に広く使用されています。 Wolfram Mathematica は非常に強力ですが、無料ではなく、研究に使用するには有料ライセンスが必要です。数千の数学関数、リアルタイムデータ、自然言語入力、その他多くのエキサイティングな機能をサポートしています。

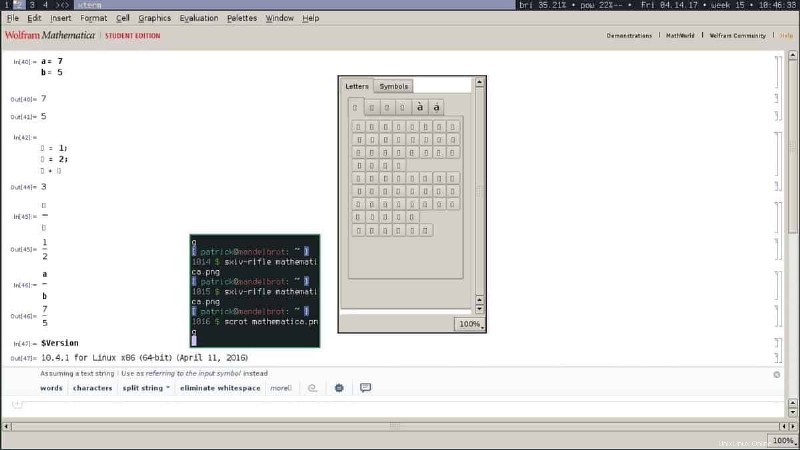
Wolfram Mathematica の機能

Wolfram Mathematica には非常に完成度の高いライブラリが付属しており、現代の計算問題を解くのに必要なほぼすべての基本関数と特殊関数が含まれています。
ディオファントス方程式、微分方程式 (ODE/PDE/DAE/DDE/SDE)、再帰関係など、幅広い連立方程式を解くことができます。
Wolfram Mathematica は、堅牢な多変量統計ライブラリ、データおよびテキストマイニングツール、制御システムライブラリ、信号処理ライブラリをユーザーに提供します。
インターフェイスは非常に汎用的で、ブロックチェーン、マイクロコントローラー、オンラインアクセスなどの最新のテクノロジーにうまく適合します。

12.マグマ

Magma は、高度な数値計算機能を使いやすく効果的なユーザーインターフェイスとシームレスに組み合わせた堅牢なコンピューター代数システムです。純粋数学の分野で広く使用されており、研究で広く取り上げられています。 Magma は、代数、数論、代数幾何学、代数的組み合わせ論の分野に関連するいくつかの種類の問題を処理できます。これはシドニー大学によって配布されており、非営利の所有ライセンスが付属しています。

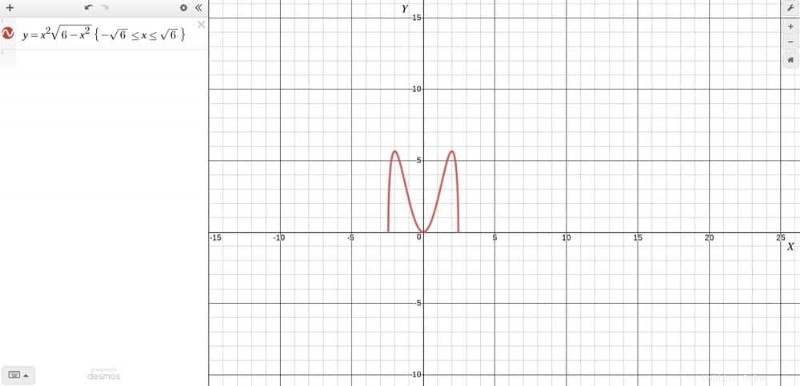
マグマの特徴

Schönhage-Strassen アルゴリズム、楕円曲線法、二次ふるい、数体ふるいなどの初歩的な数学演算用の漸近的に高速なアルゴリズムを備えています。
Magma にはデフォルトで KANT コンピューター代数システムが付属しており、代数体の便利な計算が可能です。
加群理論、線形代数、スパース行列、格子、表現理論、不変理論、グレブナー基底も扱うことができます。
Magma は、研究者が暗号アルゴリズムを扱うことを可能にし、最も一般的なアルゴリズムの最適化された実装を提供します。

13.減らす

Reduce は、物理学の研究者を対象とした堅牢なコンピューター代数システムです。複雑な物理問題を扱う人に適した選択肢となる機能の広範なリストを提供します。これは BSD ライセンスの下にあり、開発者はソフトウェアを好きなように拡張して配布することができます。 Reduce は 60 年代から開発が続けられており、世界中の物理実験室で使用されています。しかし、成長は鈍化しているようで、最後の安定版リリースは 8 年前に明るみに出ました。

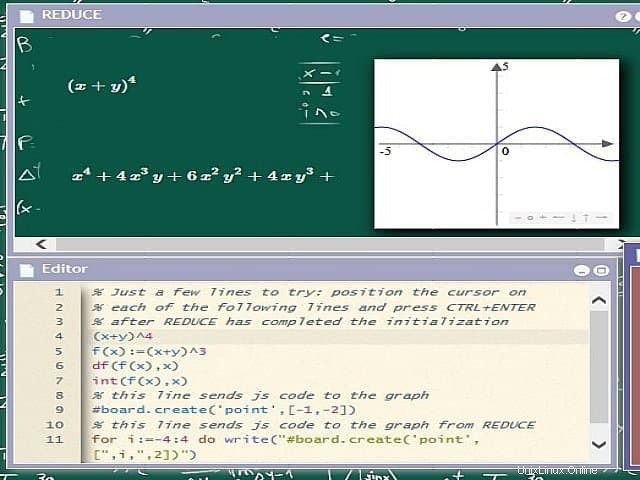
Reduce の機能

Reduce は、任意精度の数値近似手法を活用して、正確な整数および小数演算結果を提供します。
多項式、有理関数、指数関数、対数関数、三角関数、双曲線関数を、従来の微分と積分とともに処理できます。
高エネルギー物理実験で使用されるディラック行列計算を特徴とし、直感的なプログラミング言語が付属しています。
Reduce を使用すると、研究者は 2D と 3D の両方のデータセットをプロットし、さまざまな形式で出力できます。

14.パリ/GP

数論は現代のコンピューティングにおいて重要な役割を果たしており、この成長分野には数多くのアプリケーションがあります。 PARI/GP は、数論における高速計算を処理するために開発された、広く使用されている CAS であり、見逃すことのできない印象的な一連の機能を提供します。より伝統的なものに加えて、高度な関数の実装の幅広いセットが付属しており、数論の研究者とコンピューター科学者の両方が広く使用できます.

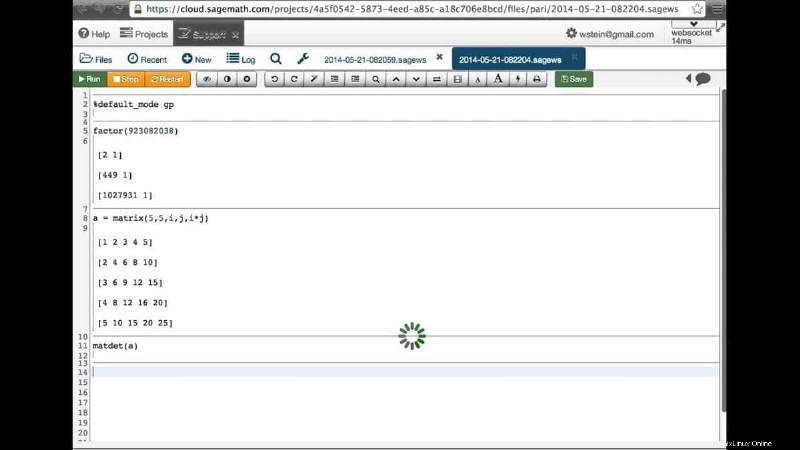
PARI/GPの特徴

PARi/GP は、因数分解、楕円曲線の計算、行列、べき級数、代数的数、その他多くの数論のトピックを扱うことができます。
PARI 機能へのアクセスを提供し、プログラム可能な電卓として使用できる最新のインタラクティブシェルを備えています。
PARI/GP は C ライブラリとしてプリインストールされているため、ユーザーは他のプログラム内で使用でき、高速な計算を実現できます。
このコンピュータ代数システムには、GP スクリプトを非常に効果的に C にコンパイルする事前構築済みの GP-to-C コンパイラが付属しています。

15.ギャップ

GAP は、計算離散代数の問題を解決するための強力なオープンソースシステムです。これは、最高のコンピューター代数システムの機能と、高レベルで直感的で便利なプログラミング言語を組み合わせたエキサイティングなプラットフォームです。 GAP は、さまざまな種類の個別の数学的問題に取り組むことができますが、計算群理論を非常に強調しています。デフォルトのライブラリは非常に広範で、すぐに使用できる数千を超える関数の実装が特徴です。

ギャップの特徴

GAP は、使いやすく直感的な驚異的なグラフィカルユーザーインターフェースを備えています。
この CAS システムにバンドルされているプログラミング言語は解釈され、実行を高速化するために簡単にコンパイルできます。
GAP は、GAP インターフェイスからアクセスできるさまざまな代数オブジェクトの大規模なクラスを含む、非常に充実したデータライブラリを提供します。
このクロスプラットフォームのコンピューター代数システムは完全にオープンソースであり、ユーザーは要件に応じてソースを拡張または変更できます。

16. SMath スタジオ

SMath Studio は、Linux 用の無料のクロスプラットフォームコンピューター代数システムです。 SMath Studio は無料ですが、オープンソースではないため、変更を許可することはできません。 C# プログラミング言語を使用して記述されており、ほぼすべての主要なオペレーティングシステムをサポートしています。また、一部のハンドヘルドデバイスとともに、Android および iOS スマートフォンプラットフォームのサポートも追加されました。シンプルで高速で効果的な Linux コンピューター代数システムを探しているなら、SMath Studio は試してみる価値があります。

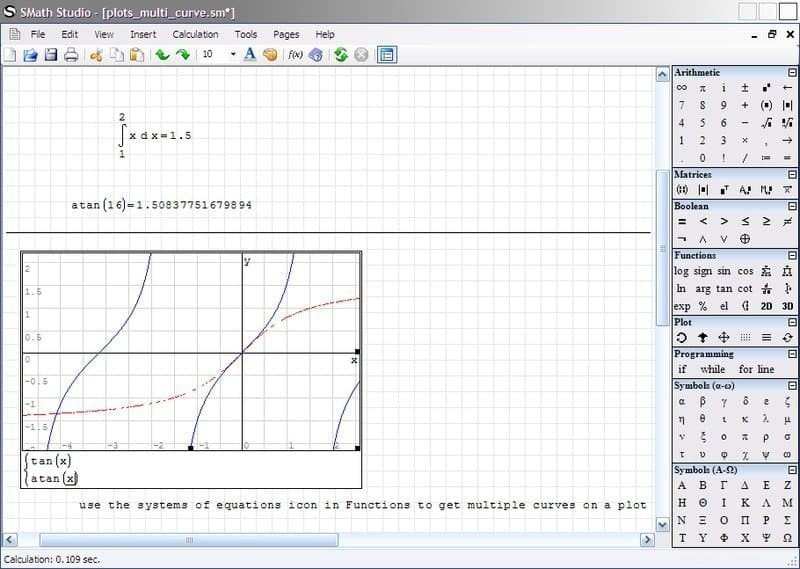
SMath Studio の機能

SMath Studio は非常に軽量で、重さは約 2 MB です。
微分方程式、連立方程式、行列演算、数値積分、その他の記号計算を解くことができます。
ユーザーは、単純な複数行のループを使用して独自の関数を定義し、プログラムを開発できます。
SMath Studio には柔軟な WYSIWYG エディターが付属しており、40 を超える言語をサポートしています。

17.公理

Axiom は、さまざまな種類の計算タスクで広く使用されている汎用のコンピューター代数システムです。これは、学術研究目的または複雑な現代の数学的アルゴリズムの開発に使用できます。 Axiom は、厳密に型付けされた数学的に正しい型階層を強調し、アルゴリズムの最適化を最大限に高めます。 Axiom は、研究者がカスタマイズされた要求に合わせてソフトウェアを拡張できるようにする、変更された BSD ライセンスを特徴としています。

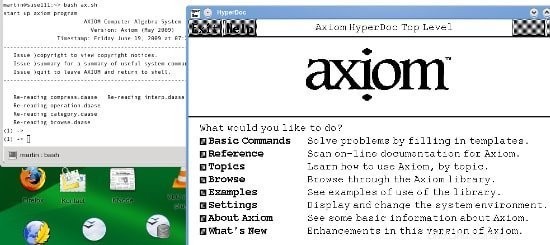
公理の特徴

Axiom は、明示的な型注釈を作成するための堅牢な型インターフェイスとヒューリスティックアルゴリズムを実装しています。
データ分析と視覚化のための 2 次元および 3 次元グラフの表示に使用できます。
Axiom には、「HyperDoc」と呼ばれる革新的なインタラクティブなブラウザースタイルのヘルプシステムが装備されています。
Axiom は、基本的な統合のための Risch アルゴリズムとともに、インタラクティブな回転および照明機能を提供します。

18. CoCoA

可換代数問題を解くのに最適なコンピューター代数システムを探しているなら、CoCoA は最適な選択肢です。これは軽量でインタラクティブなシステムであり、可換代数の計算をこれまで以上に簡単にする強力な機能を多数提供します。 CoCoALib C++ ライブラリの上にあり、ほとんどの従来の Linux コンピューター代数システムよりも高速なパフォーマンスを提供します。

CoCoA の特徴

CoCoA は、GNU Multi-Precision Library を利用することで、非常に大きな整数と有理数に取り組むことができます。
これにより、研究者は多変量多項式を効果的に処理し、Groebner 基底を扱うことができます。
CoCoA には、テキストベース、Emacs ベース、Qt ベースのインターフェースなど、多数のインターフェースのサポートが組み込まれています。
このクロスプラットフォームのコンピューター代数システムは無料で、GNU GPL ライセンスに基づいて変更できます。

19.ヤカス

Yacas、Yet Another Computer Algebra System の略は、広範囲の数値的および記号的な数学計算を効果的に実行できる汎用のコンピューター代数システムです。独自のプログラミング言語があらかじめ装備されており、基礎となる複雑な数式の高レベルの抽象化を提供します。正確な結果で任意精度の数値計算を計算でき、効率的なデータの視覚化と分析のための強力なプロット機能を提供します。

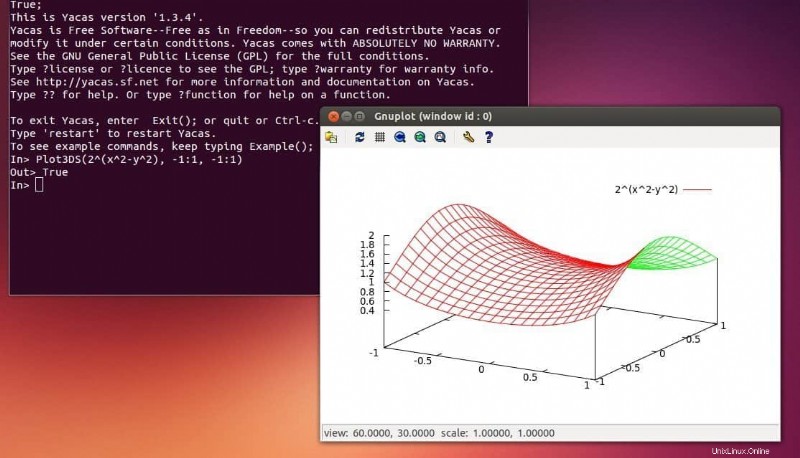
ヤカスの特徴

Yacas を使用すると、数学者は、平文形式またはバッチ入力を処理できる OpenMath のいずれかで入力を取得できます。
エディター内で呼び出すことができるスクリプトの形式で、既に実装されているアルゴリズムの膨大なセットが付属しています。
Yacas は広範なドキュメントサポートを提供しているため、この CAS を Linux 用のほとんどのコンピューター代数システムよりも速く簡単に適応させることができます。
Yacas は完全にオープンソースであり、現代の数学者の要件に合わせて変更または拡張できます。

20.フリキャス

FriCAS は、Axiom の上に構築された高度なコンピューター代数システムです。従来の微積分から幾何代数に至るさまざまな数学的計算で使用される自己完結型のツールボックスを提供します。新しいユーザーに役立つドキュメントを提供する堅牢な統合ヘルプシステムが付属しています。システムは完全にオープンソースであり、SPAD プログラミング言語を使用して簡単に拡張できます。

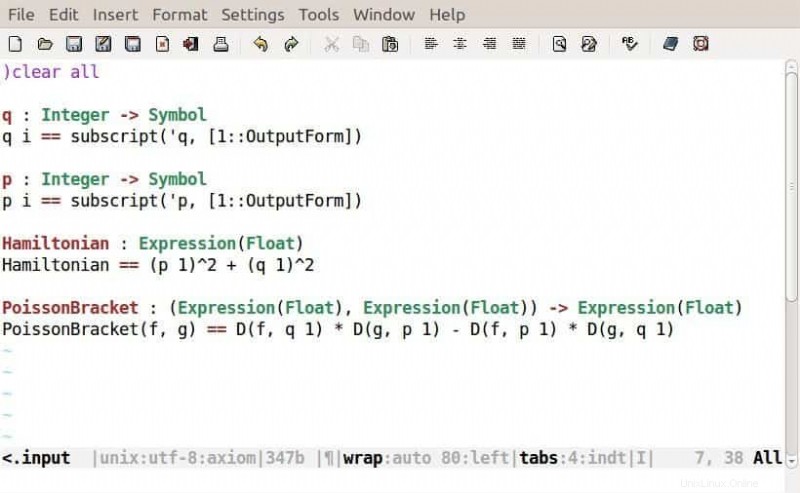
FriCASの特徴

FriCAS は、シンボリック計算用のシンプルかつ直感的なコマンドを幅広く提供し、堅牢な数値ライブラリを提供します。
革新的なインタラクティブコンソールを使用して、さまざまなタイプのデータセットを簡単にプロットできます。
FriCAS には、パターンマッチング、ベクトル、セット、マルチセット、およびハッシュテーブルのサポートが組み込まれています。
この CAS のオープンソース BSD ライセンスにより、明示的な許可なしにソフトウェアを変更またはカスタマイズすることができます。

結末

Linux は、数学者が手に入れることができる最高のコンピューター代数システムのいくつかを提供します。その結果、これらのオプションの数とバリエーションが多く、多くのユーザーを混乱させる傾向があります。彼らが毎日のコンピューティングに最適な CAS システムを見つけるのを助けるために、私たちの編集者は、Linux 用の 20 の最高のコンピューター代数システムを概説するこの有益なガイドを編集しました。うまくいけば、私たちはあなたの関心に適切に応え、あなたが始めるために必要なすべての必需品を提供することができます.以下のおすすめについてご意見をお聞かせください。さらにエキサイティングな Linux ソフトウェアガイドをお楽しみに。