このチュートリアルでは、ScientificLinuxでのベクトル代数と対応する計算について説明します。私たちの目的のために、私はその単純さと計算力のためにプログラミング言語としてPythonを選択しました。 Linuxディストリビューションには、デフォルトで、ターミナルウィンドウから呼び出されるPythonエディタ/コンパイラがあります。ベクトル代数のいくつかの概念を見てみましょう。
注：2次元または3次元の実空間でのみ作業します。
ベクトル空間の要素は、数学的な観点から、そのベクトル空間に属するいくつかの要素の配列として表すことができます。より具体的には、数値計算アプローチでは、実数のリストとして表すことができます。これには、次の3つの基本的な特性があります。
ベクトルのサイズは、次のように表されます。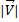 
;これはベクトルのスカラー部分です。ベクトルの大きさを計算するには、次の式を実行する必要があります。
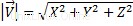
X、Y、Zはベクトル座標です。
ベクトルの方向は、ダイレクタ角度と呼ばれる座標系の各軸に対して特定の角度を持つdirectrix線によって与えられます。
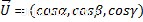
アルファ、ベータ、ガンマがベクトルディレクターの角度であり、それらの余弦がディレクターの余弦である場合、各ベクトル座標をその大きさで割ることによって計算することもできます。
同じ方向の間の2つの可能な方向の1つ。
ベクトルの代数和を作成するには、実数の代数和の同じプロパティに対応して、2つのベクトルの相同座標を追加する必要があります。次のように：
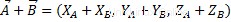ご覧のとおり、結果は同じベクトル空間に属する別のベクトルになります。
ベクトルとスカラーが与えられた場合、スカラーによる内積は、ベクトルの各座標の内積として定義されます。
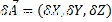
場所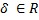 
単位ベクトル
スカラーによる製品ベクトルの直接の適用は、単位ベクトル、単位ベクトル は長さ1のノルムベクトルです。
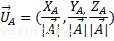
線形結合
過去の演算、代数和、積ベクトルスカラーを組み合わせると、線形結合が得られます。結果は、同じベクトル空間に属するベクトルでもあります。は：
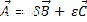
ここで、ベクトルAはベクトルBの線形結合です。およびC。
ScientificLinux7.1上のPython
ベクトル代数を実装するために、微積分言語としてPythonを選択しました。選択したテキストエディタはgeditであり、デフォルトでディストリビューションのScientificLinux7.1に付属しています。
ターミナルを使用してgeditを呼び出すか、[アプリケーション]タブのアイコンをクリックします。
まず、ベクトルを表すものとしてリストを操作する必要があり、次のように宣言する必要があります。は：
V=[2, 2, 1]
大きさを格納して値を与える変数を宣言しましょう。0を使用します。
modV=0
次に、クラスmathを使用して平方根を操作します。
import math
マグニチュードの計算：
modV=math.sqrt(V[0]**2+V[1]**2+V[2]**2)
ご覧のとおり、サブインデックスを使用して、操作するリストの項目を0から開始する必要があります。
完全なスクリプトは次のとおりです。
V=[2, 2, 1]
modV=0
import math
modV=math.sqrt(V[0]**2+V[1]**2+V[2]**2)
print (modV)
終了したら、拡張子.pyのファイルを保存し、ファイルパスを見つけて、右クリックしてターミナルウィンドウを開き、[ターミナルウィンドウで開く]必要があります。 Pythonインタープリターを呼び出す必要がある後、次のように入力します。
$ python [path]/yourfilename.py
これにより、次のようなウィンドウが開き、結果が表示されます。
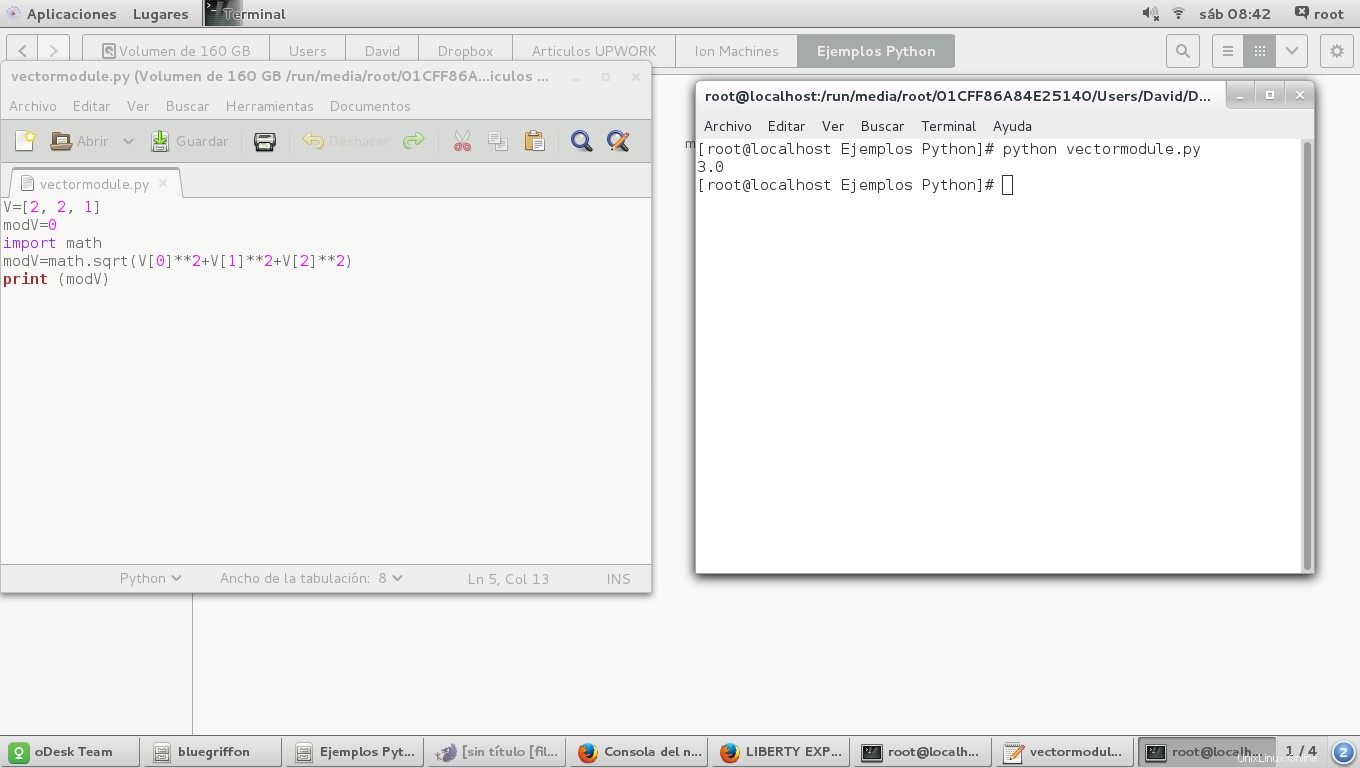
これを行う別の方法は、次のようなforループを使用することです。
for x in range (0,3):
modV+=V[x]**2
modV=math.sqrt(modV)
ここでは、Pythonインタープリターがそのように機能するため、インデント手法を使用する必要があります。
クラス数学を使用する
V=[2, 1, 2]
modV=0
import math
for x in range (0,3): #loop for calculating the magnitude
modV+=V[x]**2
modV=math.sqrt(modV)
for y in range (0,3): #loop for calculating the director cosines
V[y]=V[y]/modV
print (V)
結果は次のとおりです。
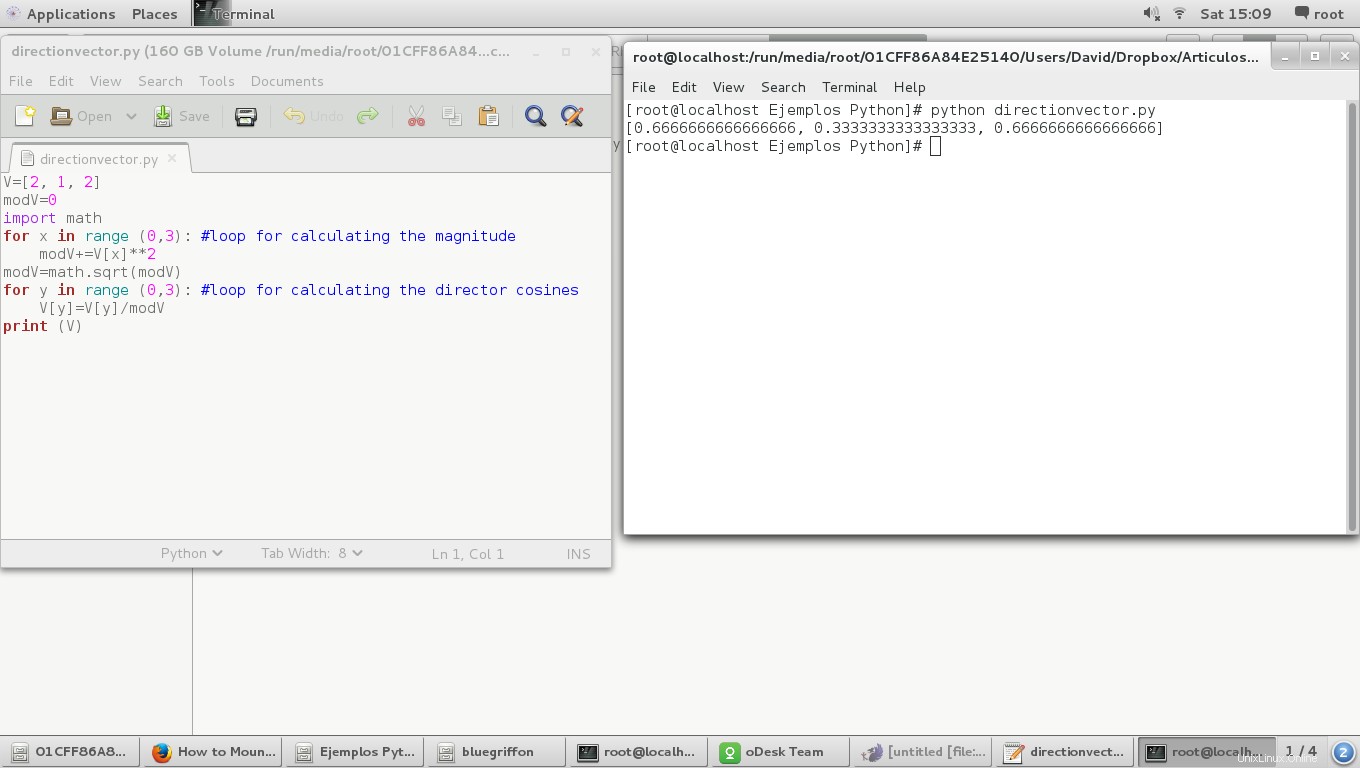
これを行う別の方法は、数学クラスの三角関数を使用することです。このように：
まず、ディレクターの角度を計算しましょう：
V=[2, 1, 2]
angles=[0,0,0]
modV=0
import math
for y in range (0,3): #loop for calculating the director angles in degrees
angles[y]=math.degrees(math.acos(V[y]/modV))
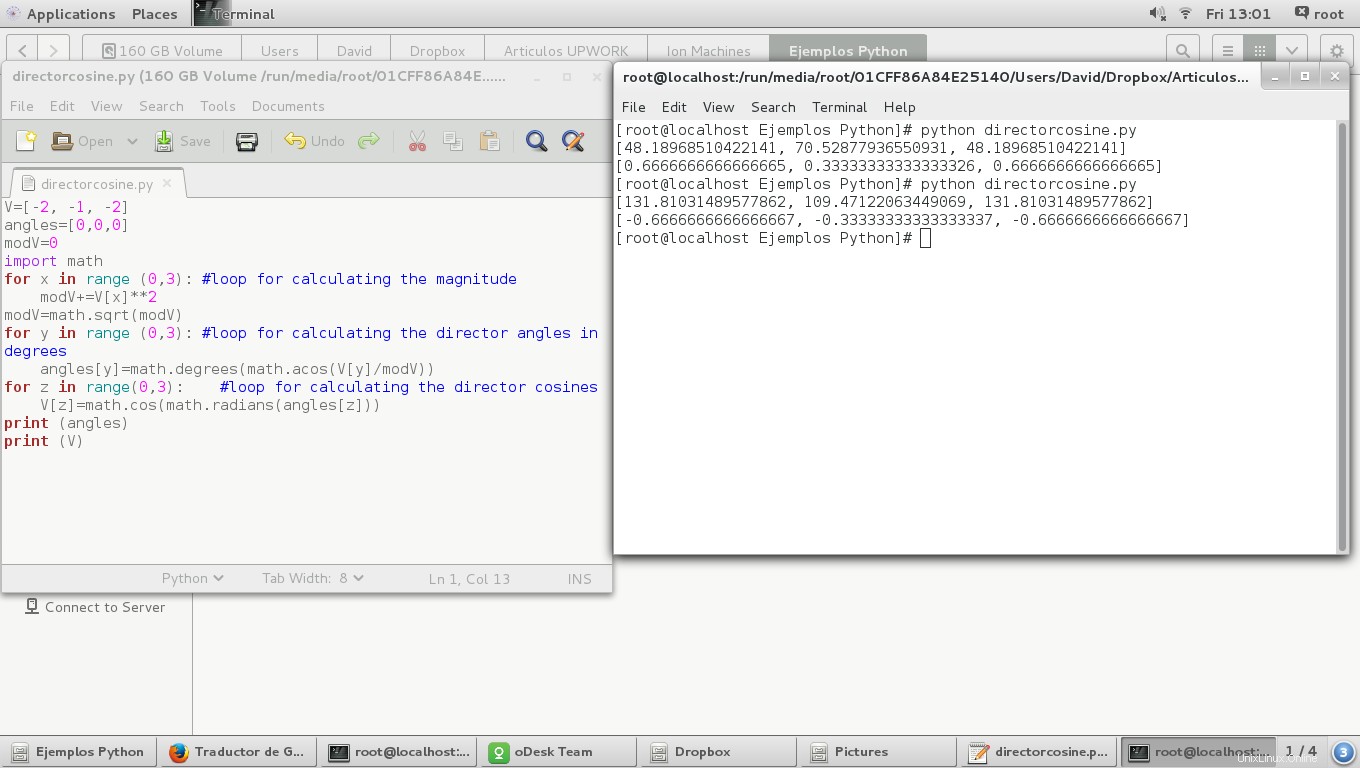
次に、ディレクターの余弦定理を計算して印刷します
for z in range(0,3): #loop for calculating the director cosines
V[z]=math.cos(math.radians(angles[z]))
print (angles)
print (V)
そして結果：
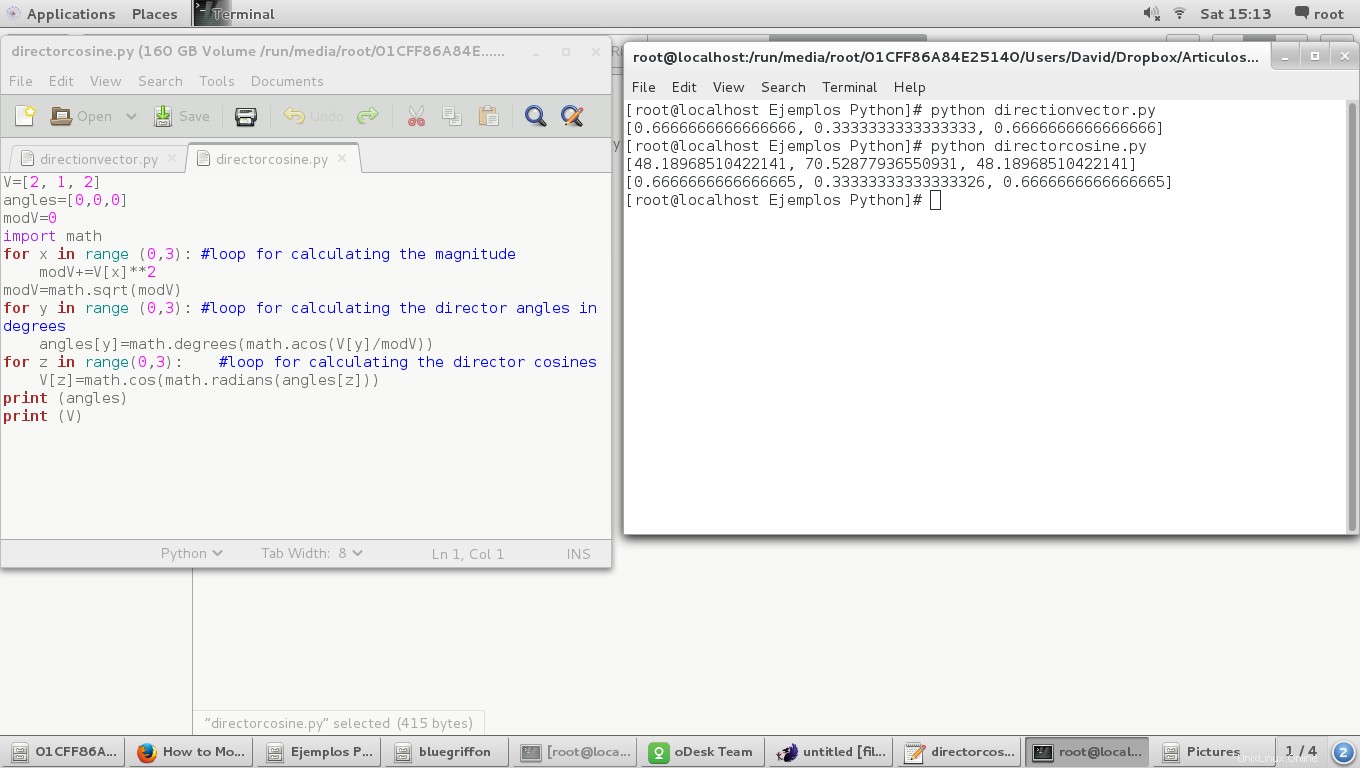
ディレクターの余弦定理が同じ値であることがわかります
ベクトルのすべての座標の符号を変更すると、本質的に、次のようにベクトルの方向が変更されます。
V=[-2, -1, -2]
angles=[0,0,0]
modV=0
import math
for y in range (0,3): #loop for calculating the director angles in degrees
angles[y]=math.degrees(math.acos(V[y]/modV))for z in range(0,3): #loop for calculating the director cosines
V[z]=math.cos(math.radians(angles[z]))
print (angles)
print (V)
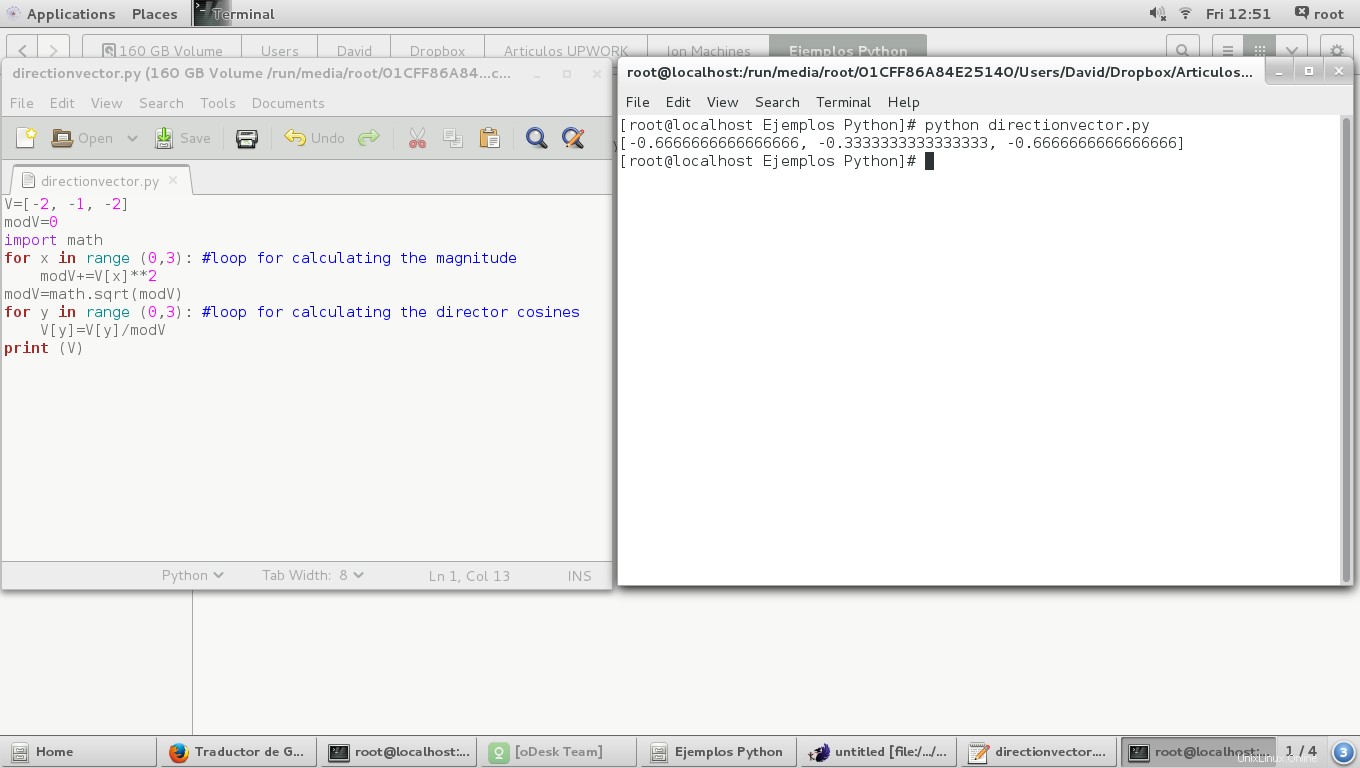
次の画像では、ディレクターの角度が180度異なることがわかります。オリジナルから
まず、代数和に含まれるすべてのベクトルを次のように宣言する必要があります。
A=[1,2,4]
B=[2,1,4]
S=[0,0,0]
ここで、AとBを合計すると、結果はSに格納されます
Pythonで2つのベクトル（リスト）を追加することは、結果のベクトルの座標ごとに「for」ループを実行することと同じであるため、次のことを行う必要があります。
for x in range(0,3):
S[x]=A[x]+B[x]
ここに、代数ベクトル和の完全なスクリプトがあります：
A=[1,2,4]
B=[2,1,4]
S=[0,0,0]
for x in range(0,3): #For loop for adding the homologue coordinate of each vector
S[x]=A[x]+B[x]
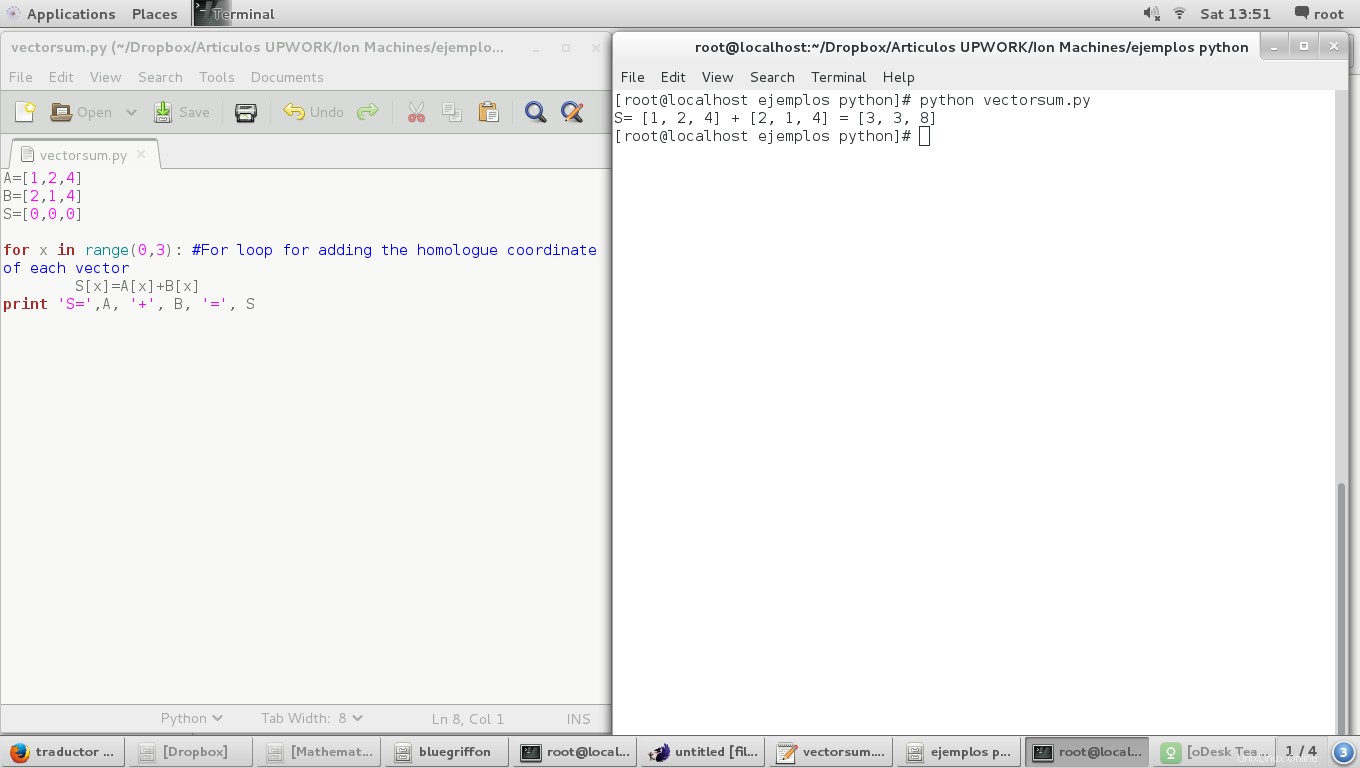
print 'S=',A, '+', B, '=', S
結果は次のとおりです。
与えられたベクトル：
A=[1,-2,3]
およびスカラー：
scalar=-2
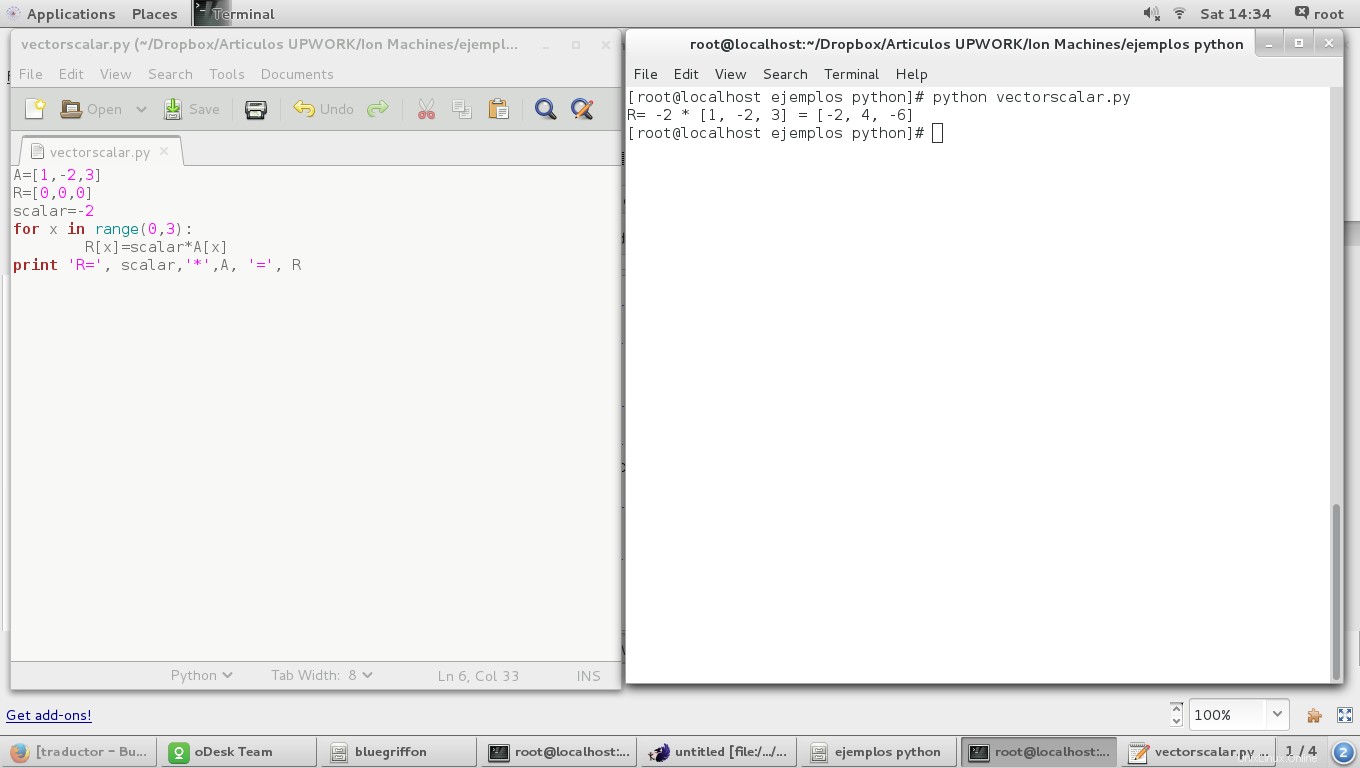
スカラーによる積ベクトルは、ベクトルの各座標の内積として定義されます。
for x in range(0,3):
R[x]=scalar*A[x]
結果は次のとおりです。
単位ベクトル
「ベクトルの大きさ」スクリプトを使用すると、次のようになります。
V=[2, 2, 1]
U=[0,0,0]
modV=0
invmodV=0
import math
modV=math.sqrt(V[0]**2+V[1]**2+V[2]**2)
invmodV=1/modV
for x in range(0,3):
U[x]=invmodV*V[x]
print 'U=',V,'/',modV,'=',U
結果は次のとおりです。
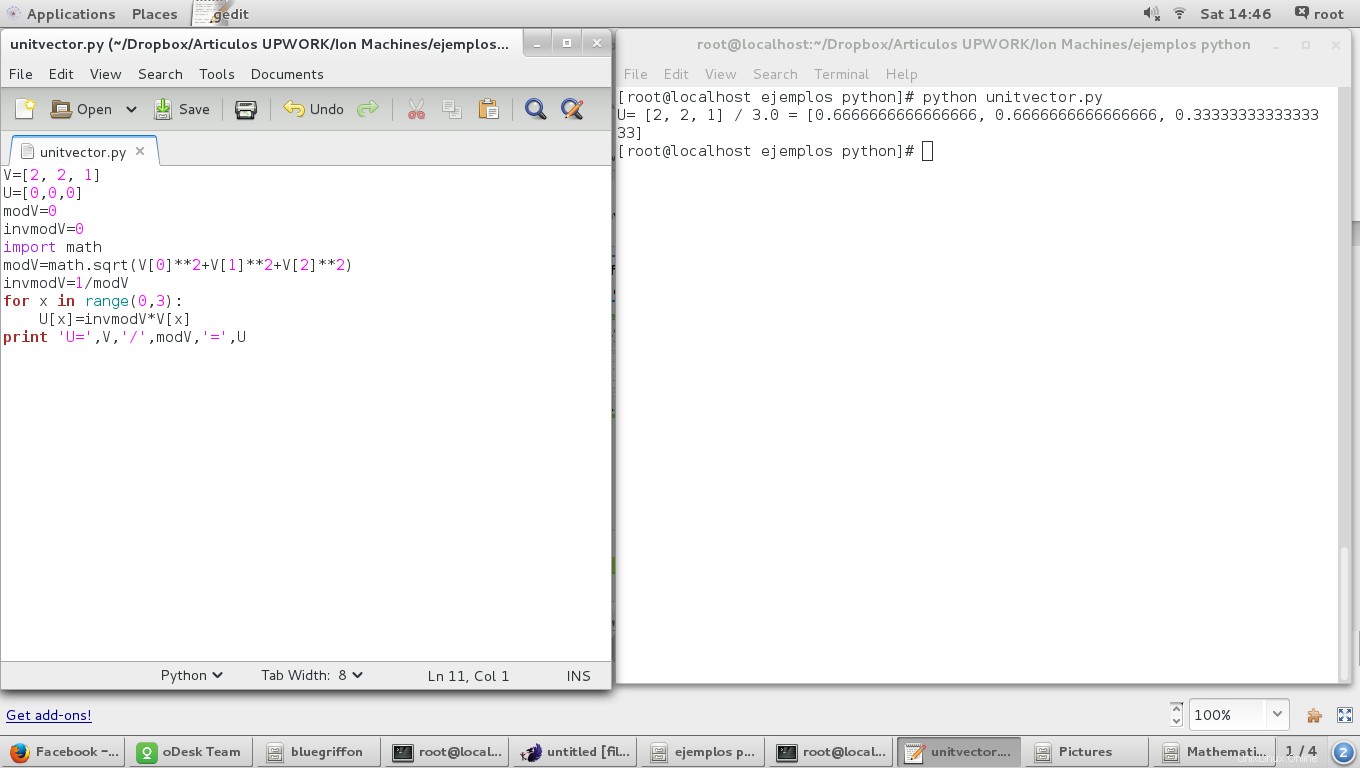
線形結合
3つのベクトルA、B、Cが与えられると、スカラー値を計算できます。スカラー値にそれぞれBとCを掛けると、ベクトルAになります。つまり、ベクトルAをベクトルBとCの線形結合として配置します。 ：
A=[7, 9, -8]
B=[1, 3, -2]
C=[-2, 0, 1]
線形結合は、連立方程式、3つのベクトルr3の場合は2つの変数（スカラー）を持つ3つの方程式、またはR3の2つのベクトルの場合は2つの変数を持つ2つの方程式につながります。これは、行列の行列式を適用することで解くことができます。ここでは、Pythonによって処理されるデータ型のためにポイントを作成する必要があります。多くの場合、線形結合に含まれるスカラーを計算すると、結果は小数点以下の桁数になり、浮動小数点演算になります。 Pythonで処理される数値データ型は、整数、実数、長整数です。したがって、ベクトルの座標を実数データ型として挿入する必要があるため、これらは実数（浮動小数点）を表します。 Pythonのデータ型のいくつかの特性を知って理解する必要があります：
- 整数は実数型よりも少ないメモリスペースを使用します。
- Realを使用した操作はIntegerよりも低速です。
ここに同じベクトルがありますが、実数型として宣言されています：
A=[7.0,9.0,-8.0]
B=[1.0,3.0,-2.0]
C=[-2.0,0.0,1.0]
したがって、これを使用すると、ベクトルを交換できるため、常にシステムソリューションを得ることができます。
最初に行う必要があるのは、ベクトル間に共面性があるかどうかです。したがって、そこにあるかどうかを確認します。線形結合です。そのために、行列式行列を実装します：
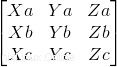
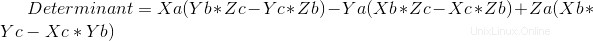
コード：
det0=A[0]*(B[1]*C[2]-B[2]*C[1])-A[1]*(B[0]*C[2]-B[2]*C[0])+A[2]*(B[0]*C[1]-B[1]*C[0]) #Main Determinant involving all vectors
この行列式がゼロ（0）に等しい場合、ベクトル間に線形依存性があり、スカラーの計算を続行できます。上記のように、連立方程式には2つの変数を持つ3つの方程式があり、互換性のあるシステムが決定されます。このシステムでは、3つの方程式のうち2つを取り、スカラー値を解く必要があります。スカラー値はそれを解決します。彼らがこれを解決しない場合、線形結合はありません。
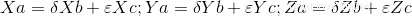
ここに完全なコードがあります：
A=[7.0,9.0,-8.0]
B=[1.0,3.0,-2.0]
C=[-2.0,0.0,1.0]
det0=A[0]*(B[1]*C[2]-B[2]*C[1])-A[1]*(B[0]*C[2]-B[2]*C[0])+A[2]*(B[0]*C[1]-B[1]*C[0]) #Main Determinant involving all vectors
if det0==0:
det1=B[0]*C[1]-B[1]*C[0] #First Determinant involving the first and second lines of the equations system
if det1==0:
det2=B[1]*C[2]-B[2]*C[1] #Second Determinant involving the second and third lines of the equations system
if det2==0:
print 'Linear Combination Unexistent'
else:
det3=A[1]*C[2]-A[2]*C[1]
det4=B[1]*A[2]-B[2]*A[1]
sc1=det3/det2
sc2=det4/det2
if sc1*B[0]+sc2*C[0]==A[0]:
print 'Scalar 1 =', sc1, 'Scalar 2 =', sc2
print A,'=',sc1,'*',B,'+',sc2,'*',C
else:
print 'Linear Combination Unexistent'
else:
det3=A[0]*C[1]-A[1]*C[0]
det4=B[0]*A[1]-B[1]*A[0]
sc1=det3/det1
sc2=det4/det1
if sc1*B[2]+sc2*C[2]==A[2]:
print 'Scalar 1 =', sc1, 'Scalar 2 =', sc2
print A,'=',sc1,'*',B,'+',sc2,'*',C
else:
print 'Linear Combination Unexistent'
else:
print 'Linear Combination Unexistent'
そして結果：
[[email protected] ejemplos python]# python lincomb.py
Scalar 1 = 3.0 Scalar 2 = -2.0
[7.0, 9.0, -8.0] = 3.0 * [1.0, 3.0, -2.0] + -2.0 * [-2.0, 0.0, 1.0]
[[email protected] ejemplos python]#
結論として、基本的なベクトル代数は、線形連立方程式および/または実数を使用した単純な算術を含む一連の演算をもたらします。別のチュートリアルでは、内積、外積、混合積などのベクトルを使用して製品を開発する方法を説明します。